 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes live video seminars, enchanting renewal songs and a thousand page illustrated codex.
 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes
live video seminars, enchanting renewal songs and a thousand page
illustrated codex.
 Return to Genesis of Eden?
Return to Genesis of Eden?
Madhusree Mukerjee Scientific American Jan 96
The Theory of Everything, or TOE, theorists believe, is hovering right around the corner. When finally grasped-the fantasy goes-the TOE will be simple enough to write down as a single equation and to solve. The solution will describe a universe that is unmistakably ours: with three spatial dimensions and one time dimension; with quarks, electrons and the other particles that make up chairs, magpies and stars; with gravity, nuclear forces and electromagnetism to hold it all together; with even the big bang from which everything began. The major paradigms of physics-including quantum mechanics and be revealed as intimately related. "Concepts of physics today will be completely changed as the story unfolds," predicts Edward Witten of the Institute for Advanced Study in Princeton, N.J. Grand promises were also heard a decade ago, when "string theory' gained favour as a TOE. Physicists crafted the theory from the idea that the object in the universe is an unimaginably tiny string.
The undulations of such strings were posited to yield all the particles and forces in the universe. These loops or segments of string are about 10-33 centimeter long and vibrate in many different modes, just as a violin string can. Each vibrational mode has a fixed energy and so by the laws of quantum mechanics can be thought of as a particle. But string theory soon ran into mathematical barriers: it frayed into five competing theories. "It's unaesthetic to have five unified theories," wryly comments Andrew Strominger of the University of California at Santa Barbara. Worse, the theories had thousands of solutions, most of which looked nothing like our universe. Asked in 1986 to summarize the TOE in no more than seven words, Sheldon L. Glashow of Harvard University, a longtime critic, exclaimed in mock anguish: "Oh, Lord, why have you forsaken me?" The "Lord," it would appear, has heard. A peculiar new symmetry, called duality, is making all the different strings twine into one another. Indeed, duality is redefining what physicists consider a fundamental particle-or string. Elementary objects now seem to be made of the very particles they create. Witten believes duality not only will lead to a TOE but also may illuminate why the universe is the way it is. "I think we are heading for an explanation of quantum mechanics," he asserts. Few critics of the theory's current claims can be heard: string mathematics is so complex that it has left behind the vast majority of physicists and mathematicians. At the same time, the world according to duality is getting even more bizarre. Strings mutate with ease into black holes, and vice versa; new dimensions blow up in different realms; and not only strings but bubbles and other membranes shimmer down the byways of the universe. The multitude of links, the researchers believe, points to a deeper entity-presumably the TOE-that explains it all. "It's like aspen trees," offers Michael J. Duff of Texas A&M University, waving at a nearby stand. "There is a root system that spreads under the ground. You see only the little bits that poke up above the surface."
A New Symmetry
The word "dual"-fast replacing "super" as the most overused word in particle theory-has many different connotations for physicists. Broadly, two theories are said to be dual if they are apparently dissimilar but make the same physical predictions. For example, if all the electrical and magnetic quantities in Maxwell's equations for electromagnetism are interchanged, one nominally obtains a different theory. But if in addition to electrical charges, the world is presumed to contain magnetic charges (such as the isolated north pole of a bar magnet), the two theories become exactly the same-or dual. Specifically, duality makes elementary and composite objects interchangeable: a particle or other entity is irreducibly fundamental or is itself made up of even more fundamental entities depends on your point of view. Either perspective ultimately yields the same physical results.
The first signs of duality appeared while physicists were working on quantum-field theories, theories that describe particles as quantum-mechanical waves spread out in space-time. In the field theory called quantum chromodynamics, or QCD, quarks are elementary particles that have a kind of charge, much like electrical charge, caned color. Color makes quarks attract one another very strongly, clumping into pairs and triads to form larger, composite particles such as protons.
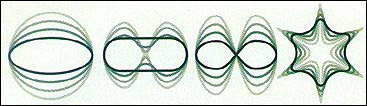
DIVERSE MODES of vibration can be induced in any
string. Quantum mechanics allows the waves to be
interpreted as particles. H loops of string about 10-33 centimeter
long are fundamental constituents of matter,
then their vibrational energies are the masses of elementary particles
such as electrons, quarks and photons.
Just as in the familiar world there are no particles with magnetic charge, there are no particles with color magnetic charge. But in 1974 Gerard 't Hoot of Utrecht University in the Netherlands and Alexander Polyakov, then at the Landau Institute near Moscow, described how fields making up quarks might knot into small balls endowed with color magnetic charge. Such clumps-which physicists visualize as hedgehog-like spheres studded with arrows representing vectors-are generically called solitons and behave like particles. Thus, a theory of quarks with color charge might also imply the existence of solitons with color magnetic charge, otherwise known as monopoles. The monopoles would be composite particles, derived from the fields of more elementary quarks. In 1977 David Olive and Claus Montonen, working at CERN near Geneva, speculated that field theories involving color might be dual. That is, instead of quarks being elementary and monopoles composite, perhaps one could think of the monopoles as being elementary. Then one might start with a field theory of interacting monopoles, finding that it gave rise to solitons that looked like quarks. Either the quark or the monopole approach to the theory should give the same physical results. Most theorists were skeptical. Even if duality did exist, it was thought impossible to establish: the mathematics of QCD is extremely hard, and it would be necessary to calculate two sets of predictions for comparison. "In physics it's very rare that you can calculate something exactly," remarks Nathan Seiberg of Rutgers University. In February 1994, however, Ashoke Sen of the Tata Institute in Bombay, India, showed that on occasion, predictions of duality could be precisely tested-and were correct. The calculation converted the string community. "Witten went from telling everyone this was a waste of time to telling them this was the most important thing to work on," Harvey chuckles. Witten, often referred to as "the Pope" by detractors of string theory, has initiated many trends in particle physics during the past two decades. Meanwhile Seiberg was developing an extremely helpful calculational shortcut for studying QCD. His work was based on supersymmetry. Supersymmetry is the idea that for each kind of particle that constitutes matter, there should be a related particle that transmits force, and vice versa. The symmetry has yet to be found in nature, but theorists frequently invoke its powers. Seiberg was able to show, by using supersymmetry to constrain the interaction between particles, how some hitherto impossible calculations in QCD might be done. He and Witten went on to demonstrate that versions of QCD that include supersymmetry are dual. There is an immediate, startling benefit. QCD is difficult to calculate with because quarks interact, or "couple," strongly. But monopoles interact weakly, and calculations with these are easy. Duality would allow theorists to deal with monopoles-and automatically know all the answers to QCD. "It's some kind of magical trick," Harvey says. "We don't understand yet why it should work." Armed with duality, Seiberg and Witten went on to calculate in great detail why free quarks are never observed in nature, verifying a mechanism put forth in the 1970s by t'Hooft and Stanley Mandelstam of the University of California at Berkeley. Of course, the validity of all this work hinges on the assumption that supersymmetry exists. Still, Seiberg hopes that, ultimately, duality will prevail even if supersymmetry is absent, so that "the qualitative results will be true even if the quantitative results depend on supersymmetry." Duality is, however, much more than a calculational tool: it is a new way of looking at the world. "Something thought of as composite becomes fundamental," Harvey points out. And vice versa. Even the normally conservative Seiberg has not been able to resist speculating that perhaps the quarks are solitons, duals of some other truly elementary particles that are even smaller.
Stringing Strings Together
The concept of duality may have grown out of field theories, but as Sen observes, "duality is much more natural in string theory." It is also more versatile. Duality can unite strings of different kinds, existing in different dimensions and in space-times of different shapes. All these feats are allowing string theory to overcome its limitations and rise to the status of a TOE.
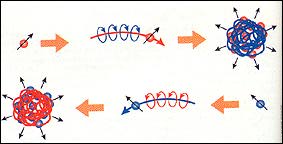
DUALITY, a type of symmetry, makes it possible
to view composite entities as equivalent to fundamental particles,
and vice versa. For example, a quark has a kind of charge called
color (red). Moving electrical charges generate magnetic fields;
likewise, moving quarks generate color magnetic fields (blue).
Sometimes many quarks can tangle into a composite object, called
a monopole, that has a color magnetic charge (top right). Because
of duality, however, it is possible to think of a monopole as
a fundamental particle (bottom right). Monopoles in turn can clump
to form quarks-which are now composite objects (bottom left).
The arrows (black) signify properties of the particles that are
vectors, such as angular momentum.
Earlier in its evolution, string theory had failed as a unified theory because of the many types of strings that were posited, as well as the embarrassing multiplicity of answers that it gave. This plenitude has its source in yet another peculiarity of string theory-it is consistent only if strings originally inhabit a 10-dimensional space-time. The real world, of course, has four dimensions, three of space and one of time. The extra six dimensions are assumed to curl up so tight that they pass undetected by large objects such as humans-or even quarks. "Think of a garden hose," suggests Brian R. Greene of Cornell University. "From a distance it looks one-dimensional, like a line. If you get close, you see it's actually a two-dimensional surface, with one dimension curled up tight." Unhappily for string theorists, the extra six dimensions can curl up in very Many different ways: "Tens of thousands is the official estimate," Strominger quips. Each of these crumpled spaces yields a different solution to string theory, with its own picture of the four-dimensional world-not exactly what one wants from a TOE. A type of duality called mirror symmetry found in the late 1980s has helped lessen tills problem by merging some of the alternative solutions. Mirror symmetry revealed that strings in two different curled spaces sometimes yield the same particles. For example, if one dimension becomes very small, a string looped around that dimension like a rubber band around a hose might create the same particles as a string moving around a "fat" dimension. The size to which a dimension shrinks is rather similar, in string theory, to another parameter: the strength with which particles interact. In 1990 Anamaria Font, Luis E. Ibanez, Dieter Last and Fernando Quevedo, collaborating at CERN, suggested that something like mirror symmetry also exists for coupling strengths. just as large spaces can have the same physics as small ones, perhaps a string theory with large coupling could give the same results as another having small coupling. This conjecture related string theories in the same way that duality worked for field theory. Moreover, from afar, strings look like particles, so that duality in string theory implies duality in field theory, and vice versa. Each time duality was tested in either case, it passed with flying colors and helped to draw the two realms closer together. Meanwhile duality was emerging from a completely different quarter - supergravity. This unified theory was an attempt to stretch Einstein's gravity to include supersymmetry. (in contrast, string theory tried to modify particle theory to include gravity.) In 1986 Duff, then at Imperial College, London, was able to derive a picture for supergravity that involved vibrations of an entirely new fundamental entity: a bubble. Whereas strings wiggled through 10 dimensions, this bubble floated in 11. "The vast majority of the string community was not the least interested," Duff recalls - most likely because no one knew how to do calculations with this bubble. Still, he continued to work on diverse theories involving closed membranes. He found that a five-dimensional membrane, or a "five-brane," that moved through a 10-dimensional space could serve as an alternative description of string theory. The five-brane could wrap itself around an internal curled space, like a skin around a sausage. But if this internal space shrank to nothing, the bubble ended up looking like a string. Duff suggested that this convoluted string was actually the same as the ones in string theory, positing a "string-string" duality. At the same time, Christopher M. Hull of Queen Mary and Westfield College and Paul K. Townsend of the University of Cambridge were hypothesizing about many generalizations of duality in string theory. "Neither group paid much attention to the other's paper," Duff says, with a gleam in his eye.
Explosion of Dualities
That is, until March 1995, when matters came to a head at a conference at the University of Southern California. Witten gave the first talk of the day, pulling together evidence for duality from diverse realms. He recognized that Hull, Townsend and Duff were all talkng about the same idea and went on to conjecture that Duff's bubbles in 11 dimensions were solitons of a particular string in 10 dimensions. After Witten, Seiberg spoke. "Natty [Seiberg] was so impressed by Witten's talk," chuckles John H. Schwarz of the California Institute of Technology. "He said, 'I should become a truck driver."' But Seiberg also presented many new results, prompting Schwarz-one of the founders of string theory-to begin his talk with, "I'll get a tricycle." An explosion of activity followed and has continued unabated. Every day scientists log on to the electronic preprint library at Los Alamos National Laboratory to find some 10 new papers in the field. "It's the first thing you do every morning," remarks Anna Ceresole of the Polytechnic of Turin. "like reading the newspaper." Scattered and curious evidence for duality is turning up, relating strings and bubbles to solitons of all kinds and shapes. One soliton, which resembles a hairy caterpillar, with vector arrows pointing out all along a line, turned out to be dual to a fundamental string. (it is also similar to a cosmic string, a fad in cosmology began by Witten a decade ago.) Different kinds of strings squeezed into the real world-four dimensions-also proved dual. "Things happen for different reasons, yet they agree," Seiberg remarks. "It feels like magic." There is a method behind the mad hunt for dualities. "Many string theories are not realistic," Sen points out. "We need to understand all of them to find the real one." Duality serves to connect, and therefore to reduce, the number of options. Witten believes the five string theories involving 10 dimensions that now prevail will all turn out to be reflections of an ultimate, supreme, quantum string.

REDUCING DIMENSIONS of a space can be achieved
by pasting its edges together and shrinking it. For example, a
two dimensional sheet of rubber is first curled into a cylinder,
and the curled dimension is then shrunk When thin enough, the
cylinder looks like a (one dimensional) line. Twisting around
this length of "hose" and sticking its ends together,
one gets a doughnut shape. The radius of the doughnut can be shrunk
until it is small enough to approximate a point-a zero dimensional
space. Such changes could explain why the extra dimensions of
space-time that string theory says must exist are too small to
be detectable.
Duff has even proposed a "duality of dualities"-the duality between spaces, and that between elementary and composite objects, might turn out to be connected. Among the most peculiar predictions of such ideas is that the size of a curled space influences the strength with which particles interact, and vice versa. So if an internal dimension is big, coupling between particles might also be large. Besides, Susskind explains, "As you go from place to place, the size of the internal dimension may vary." If a curled dimension blows up, in some far corner of the universe, space-time acquires a new, fifth dimension. Where it squeezes tight, as in our immediate environment, quantum effects appear. Indeed, the fundamental scale associated with quantum theory, called Planck's constant, is intimately entwined with duality: it relates, for example, the mass of a particle or string with that of its dual. "That is the most compelling evidence for me that string theory might teach us about quantum mechanics," remarks Stephen H. Shenker of Rutgers. "Suddenly, dimensions are changing, dimensions of fundamental objects are changing, wrapping around, anything goes," Duff shakes his head in wonder. One more suggestion from Townsend is a kind of "democracy"-the membranes turning up as solitons of string theory might all be fundamental objects, having the same status as strings. That idea has yet to catch on with the Americans, who point out that calculations with membranes still do not make sense. As Cumrun Vafa of Harvard University notes doubtfully, "It's kind of coming in sideways. You never know."
Black Holes
If that were not enough, a connection emerged last April between strings and black holes-promising to overcome the second major embarrassment in string theory. Strominger, Greene and David R. Morrison of Duke University found that black holes help to connect perhaps thousands of the tens of thousands of solutions to string theory in a complex web. The connections make the problem of finding the "right" solution to string theory-that describing our universe-much easier. In a sense, black holes have been lurking at the edges of string theory all along. If enough mass accumulates in one place, it collapses under its own gravitational pull to create a black hole. But as Stephen W. Hawking of the University of Cambridge has argued, a black hole-which usually absorbs everything, even light-may also radiate particles, slowly losing mass and shrinking. If the original mass were made up of strings, the decay would ultimately lead to an object with zero size-an "extremal" black hole, looking in fact rather like a particle. Susskind protests that these tiny black holes are nothing like the collapsed stars that astrophysicists search for: "Andy's [Strominger's] work is great, but calling these things black holes is I think a bit of hype." (Susskind's own latest paper is entitled "The World as a Hologram.") in fact, extremal black holes-or black bubbles or black sheets-are simply clumps of string fields, otherwise known as solitons. Strominger was investigating how extremal black holes behave when a dimension of space-time curls up very tight. imagine taking an infinitely long hose, looping it around and sticking the ends together so that it resembles a doughnut. In this way, both dimensions of the surface of the hose can be shrunk, creating a much smaller space (that still has no boundaries). Now suppose that the doughnut becomes very thin at one point. As it pinches in, Stromanger found that some black holes, made of membranes wrapped around the scrunched dimension, become massless. He decided to include these objects in his calculations, as quantum-mechanical waves. Two miraculous things happened. Earlier calculations in string theory had always failed when the hose thinned to a line, but the quantum-mechanical black holes made the mathematics work out fine even in this extreme case. The real savior, Horowitz explains, is quantum physics: "In classical physics, an electron falling into the point charge of a proton gives you infinities. Only when you add quantum mechanics do you see that the electron goes into orbit." Another consequence was that large numbers of the massless black holes appeared: the system underwent a phase transition, much like vapor condensing to water. The phase transition mirrored a change in the doughnut itself. It tore open at the thinnest part-violence that physicists and mathematicians have always shrunk from-and remolded into a sphere, an alternative way of curling up a two-dimensional sheet. Thus, two very different curled spaces in string theory were connected. "Mathematicians don't like it, because it involves tearing," Strominger admits. "But quantum effects smooth it out." Different kinds of tears may ultimately turn out to relate thousands of solutions to string theory. With the internal spaces thus linked, strings can then find the "special" one by moving around among them. just as water freezes in the Arctic and vaporizes in the Sahara, strings can choose a configuration suited to their environment. Finding the right solution then becomes a dynamical problem. Somewhere in the universe, Strominger speculates, there might be a droplet in which strings have found a different internal space. On entering the droplet, black holes would turn into strings. And strings into black holes. In our immediate surroundings, such droplets might appear fleetingly as virtual universes, which exist for microscopic fractions of time and die away before they become evident.
The Theory
Despite these flights of fancy, the physicists come down to earth long enough to caution that the ultimate theory is still far off. Even the optimist Vafa, who has bet Witten a scoop of ice cream that string theory will be solved by the end of the century, believes that a true understanding will take decades to emerge. "By the time we find a beauful formulation, it might not be called a string theory anymore," Schwarz muses. "Maybe we'll just call it 'the Theory."' (Claims of finding the TOE met with so much ridicule in the 1980s that string theorists are now allergic to that sobriquet.) Not everyone is convinced that the Theory is around the comer. "Coming from the string-theory clan, the reports are as usual loaded with overstatements," 't Hoot acidly retorts. An immense problem is that there may never be any experimental tests for strings. No one can even conceive of a test for something so minute: modern equipment cannot probe anything smaller than 10-16 centimeter. Theorists pray that when the Large Hadron Collider at CERN starts operating in 2005, supersymmetry, at least, will be discovered. "It will be one of the nicest ways for nature to have chosen to be kind," says Witten (echoing Einstein's faith that God is not malicious). But even if supersymmetry shows up, another nagging problem will remain. In the real world, the familiar four-dimensional space-time is flat; the kind of imperfect supersymmetry that theorists attribute to nature, however, makes space-time curl up impossibly tight in all dimensions. Witten has a fantasy for getting around this impasse, which relies on duality between theories in different dimensions. Perhaps one can begin with a universe in which only three dimensions are initially flat-one of the four we know is still curled up. Such space-times have peculiar but pleasant properties that allow the problems with supersymmetry to be fixed. Ultimately, the fourth dimension might be induced to expand, leading to a world like the one we know. "Witten's suggestion is pretty wild," Schwarz grins, "but he might be right." The peculiarity of gravity also raises many difficult questions. Einstein found that gravity arises from the curvature of space-time. Therefore, to quantize gravity is to quantize space and time. In that case, Horowitz argues, "maybe there is no meaning to space and time, and maybe these emerge as some approximate structure at large distances." String theory is a long way from meeting such expectations. Besides, the Theory will need to be able to describe the most extreme circumstances, such as the genesis of the universe or the environment inside a black hole. "String theorists tend to trust their theory blindly, claiming it can deal with everything," states 't Hooft with finality. "in reality, they don't understand gravitational collapse any better than anybody else." But string theorists, dazzled by the mathematical riches glinting within reach, seem undeterred by any criticism. Pierre M. Ramond of the University of Florida tries to explain: "It's as if you are wandering in the valley of a king, push aside a rock and find an enchanted staircase. We are just brushing off the steps." Where the steps lead is unknown-so the adventure is all the more thrilling Evening falls in Aspen. As the setting sun lights up the tree minks and leaves in clear yellow, the physicists continue an argument they have started over dinner. This time, it is about the wave function of the universe, a direct attempt to describe the latter as a quantum-mechanical object. "In my own opinionated, uneducated, ignorant view, I personally think it's a lot of crap,' Susskind vents: Horowitz, who along with others, has constructed such wave functions, laughs out loud. The air starts to chill, and the quaint street-lamps glow brighter in the gathering darkness. But the physicists seem in no hurry to retire.
The Mathematics of Duality
Using intuition, analogies and a kind of free-flowing mathematics inspired by nature, physicists have solved some long-standing problems in classical mathematics. They are also forcing open a new branch of mathematics, called quantum geometry. "The physicists are telling us where to look," remarks John Morgan, a mathematician at Columbia University. "It's frustrating. We don't have the access they do to this kind of thinking." In 1990 Edward Witten of the Institute for Advanced Study in Princeton, NJ., was awarded the Fields Medal - the Nobel of mathematics-for the manifold ways in which he had used theoretical physics to unravel mathematical puzzles. A key concept from physics, supersymmetry, turns out to connect intimately with modern geometry. "It's very surprising," remarks David R. Morrison of Duke University. The latest triumph of supersymmetry is a means of classifying four-dimensional spaces. These dimensions, which pertain to the real world, are curiously also the most complex. Simon K. Donaldson of the University of Oxford had shown in 1982 how to use quantum field theories to count the number of holes in a four-dimensional space and thus to classify it topologically. (For example, a sphere, a doughnut and a pretzel all belong in different categories of two-dimensional surfaces because they contain different numbers of holes.) But the calculations were horrendous because of the intractable nature of the field theories. In 1 994 Nathan Seiberg of Rutgers University and Witten pointed out that the results of one supersymmetric quantum-field theory could be provided by another, via a symmetry called duality. Thus, easy calculations might suffice to obtain the results of very difficult ones. Witten provided an equivalent set of numbers that could be calculated almost 100 times faster than the "Donaldson numbers." "Seiberg-Witten theory opened up the field and allowed us to answer most of the outstanding questions completely," Morgan says. Duality of a different kind, called mirror symmetry, has illuminated another vexing question. Mathematicians want to know how many curves of a given complexity can be drawn in a particular space. The problem is especially difficult to solve for convoluted curves. But Brian R. Greene of Cornell University and Ronen Plesser of Hebrew University of Jerusalem found that strings inhabiting two apparently unrelated spaces can yield the same results. Using this mirror symmetry, Philip Candelas of the University of Texas at Austin and others were able to tell the results of virtually impossible calculations in one space by looking to the mirror space-thus deriving the long-sought numbers.

ELIMINATING HOLES in closed spaces was thought
impossible in mathematics, but physicists have found a way. A
doughnut and a sphere are both ways of curling up a two-dimensional
surface, but they differ in the number of holes they contain.
(A doughnut has one; a sphere has none.) If part of the doughnut
thins to a point, however, the rest of it can be separated. The
doughnut can then be remolded into a sphere.
Indeed, string theory yields many more insights than classical mathematics can accommodate. The contributions that are commonly cited are only those that appear when strings are shorn of quantum mechanics. Quantum strings undulate in a host of spaces that mathematicians have yet to construct. Moreover, Greene, Morrison and Andrew Strominger of the University of California at Santa Barbara have shown that quantum effects make it possi- ble for spaces with different numbers of holes-such as a doughnut and a sphere - to transform smoothly into one another, a no-no for mathematicians. (The standard rules for manipulating spaces allow them to be stretched or compressed, but no holes can be opened or closed in them.) The study of such spaces is becoming the brand-new field of quantum geometry. The findings have rejuvenated the venerable disciplines of algebraic geometry and number theory. "These are core subjects in mathematics," states Shing-Tung Yau of Harvard University (another recipient of the Fields Medal). "if you open up a new domain here, you expect to have a lot of influence on the rest of mathematics." A major stumbling block is that mathematicians have not proved the results from string theory to their satisfaction. Yet the mathematicians agree that physicists with their questionable methods are getting at mathematical truths. "We can't free ourselves of rigor, or the field will fall apart," Morgan explains. But rigor can also be a burden, keeping mathematicians from the leaps of faith that physicists blithely make. "Are we going to wait for physicists to tell us again where to look?" he asks. "Or are we going to get to a state where we have access to that intuition?"
Into the Eleventh dimension (extract) New Scientist 18 Jan 97 Michio Kaku
Remember that at some of the finest minds of this century have been stumped by the problem of creating a "Theory of Everything'. Einstein summed up the problem when he said- 'Nature shows us only the tail of the lion. But I do not doubt that the lion belongs to it even though he cannot at once reveal himself because of his enormous size." The tail is what we see in nature, which can be described by the four fundamental forces-,gravity, electromagnetism and the strong and weak nuclear forces. The lion is the ultimate theory that will unify them in one short cquation. Today, physicists believe that the first force, gravity, can be described by Einstein's general relativity, based on the smooth warping of the fabric of space-time. This Is an elegant theory that describes the macroscopic world of black holes, quasars and the big bang. But gravity has stubbornly refused to unite with the other three forces, which are described by quantum theory. Here, instead of the smooth fabric of space- time, we have the discrete world of packets of energy, or quanta. The form of quantum theory that goes furthest in describing matter and its interactions is the Standard Model, which is based on a bizarre bestiary of particles such as quarks, Ieptons and bosons. The Standard Model may be one of the most successful theories in science, but it is also one of the ugliest, Its inadequacy is betrayed by some 19 arbitrary constants not derived by any kind of theory that have to be put in "by hand," to make the equations work. Capturing the "lion", which unites these two great theories, will be a crowning achievement for physics. But while Einstein was first to set off on this noble hunt, tracking the footprints left by the lion, he ultimitely lost the trail and wandered off into the wilderness.
Crazy departure
Today, however, physicists are following a different trail-the one leading to superstring theoy. Unlike previous proposals, it has survived every blistering mathematical challenge ever hurled at it. Not surprisingly, the theory is a radical-some Might Say crazy-departure from the past, being based on tiny strings vibrating in 10-dimensional space time. To understand how going to bigber dimensions can help to unify Iower dimensions, think back to how the Romans used to fight wars. Without radio communications and spy planes, battles were horribly confused, raging on many fronts at the same time. That's why the Romans always leapt into 'hyperspace"- the third dimension-by seizing a hilltop. From this vantage point, they were able to survey the two-dimensional battlefield as a single, unified whole,. Leaping to higher dimensions can also simplify the laws of nature. In 1915, Einstein changed completely our notion of gravity by leaping to the extra dimension of time. In 1919, the German mathematician Theodor Kaluza added a fifth dimension and in so doing unified space-time with Maxwell's equations for electromagnetism. This triumph was largely forgotten amid the frenzy of interest geticrated by quantum mechanics, Only in the 1980s did physists return to this idea to create superstring theory. In superstring theory. the subatomic particles we see in nature are nothing more than different resonances of the vibrating superstrings, in the same way, that different musical notes emanate from the different modes of vibration of a violin string, (These strings are very small-of the order of 10^-35 metres.) Likewise, the laws of physics-the forces between charged particles, for example-are the harmonies of the strings; the Universe is a symphony of vibrating strings. And when strings move in 10-dimensional space-time, they warp the space-time surrounding them in precisely the way predicted by general relativity. So strings simply and elegantly unify the quantum theory of particles and general relativity. Better still, gravity is not an inconvenient addition. "Unlike conventional quantum field theory, string theory requires gravity," Witten has said. "I regard this fact as one of the greatest insights, in science ever made." But, of course, all this takes, place in 10 dimensions. Physicists retrieve our more familiar 4-dimensional Universe by assuming that, during the big bang, 6 of the 10 dimensions curled up (or "compactified') into a tiny ball while the remaining four expanded explosively, giving us the Universe we see. What has consumed physicists for the past ten vears, is the task of cataloguing the different ways in which these six dimensions can compactify. Their task has been especially difficult because mathematician's have not worked out the topology and properties of these higher-dimensional universes. The physicists have had to blaze the trail and invent entirely new areas of mathematics. These efforts have revealed millions of cornpactifications, each of which yield a different pattern of quarks, efectrons atid so on. As we have seen, the first frustrating problem with superstring theory is that physicists do not understand where strings come from. To make matters worse, there are five string theories that unify quantum theory with relativity. This is an embarrassment of riches. Each competing theory looks quite different from the others. One, called Type 1 string theory, is based on two types of stnng: open strings, like short strands with two ends, and 'closed strings', in which the ends meet to form a ring. The other four have only closed strings. Some, such as Type 2b generate only left-handed partcles, which spin in only one direction. Others, such as'Type 2a, have left and right-handed particles.
Today's excitement has grown from the finding that if we postulate the existence of a mysterious M-theory in 11 dimensions we can show that the five competing string theories are actually different versions of the same thing. Like a Roman general surveying the battlefield from the third dimension, physicists today stand on tne hilltop of the 11th dimension and see the five superstring theories below, unified into a simple, coherent picture, representing different aspects of the same thing.
Trackng lion
The first step towards this advance came two years ago when Witten and Paul Townsend of the University of Cambridge showed that string theory in 10 dimensions was equivalent to M-theory in 11 dimensions with one dimension curled up. Since then, all five theories have been shown to be equivalent. So at last physicists know where superstrings come from: they originate in the 11th dimension from M-theory. M-theory also predicts that strings coexist with membranes of various dimensions. For example, a particle call be defined as a zero-brane (zero-dimensional object). A string is a one-brane, an ordinary membrane like a soap bubble is a two-brane, and so on. (Using p to represent the dimension of the object, one wag dubbed this motley collection "p-branes".) When these p-branes vibrate or pulsate, they create new resonances, or particles, which were missed in earlier formulations of superstrings. The name "M-theory' was coined by Witten: m perhaps stands for "membrane', or the "mother of all strings". To see how this all fits together, imagine three blind men hot on the trail of Einstein's lion. Hearing it race by, they give chase and desperately grab at it, hanging onto the tail for dear life, one feels its one-dimensional form and loudly proclaims, its a string. The lion is a string." The second man grabs the lion's ear. Feeling, a two-dimensional surface, he calls out 'No, no, the lion is really a two-brane.' The third blind man, hanging on to tne lion's leg, senses a three-dimensional solid, and shouts, "You're both wrong. The hon is a three-brane!" They are all right. Just as the tail, ear and leg are different parts of the same lion the string a nd various p-branes appear to be different parts of M-theory, Townsend calls it 'p-brane democracy'. The acid test for any theory is that it must fit the data. No matter how original and elegant superstring theory is, it will stand or fall on whether it describes the physical Universe. Either it is a Theory of Everything, as its advocates hope, or it is a theory of nothing. There is no in-between. So theoretical physicists must answer the second question: is our Universe, with its strange collection of quaks and subatomic particles, among the solutions of superstring theory? This is where it runs into an embarrassing problem, which is that physicists have been unable to find all it's four-dimensional solutions. The mathematics have been fiendishly difficult - too hard for anyone to solve completely.
In general, there are two types of solutions. So far only the first class, called "perturbative" solutions, have been found. Across all branches of physics, theorists faced by an equation they cannot solve reach for well-established ways to find approximate solutions,. in superstring theory, millions of these perturbative solutions have been catalogued. Each one correspponds to a different way in which to curl up 6 of the 10 dimensions. However, none of them precisely reproduces the pattern of quarks, leptons and bosons in the Standard Model, although some come close So, many believe that the Standard model may be found among the second class of solutions, the "non-perturbative" solutions. But non-perturbative solutions are generally among the most difficult of all solutions in physics. Some physicists despaired of ever finding non-perturbative solutions of superstring theory; after all, even the non-perturbative solutions of simple four-dimen.sional theories are completely unknown, let alone those of a complicated 10-dimensional theory. How does M-theory help to solve this intractable problem? The answer lies in a startling tool called "duality". Simply put, in M-theory there is a duality, or simple mathematical relationship, between the perturbative and non-perturbative regions. This allows us at last to take a peek at this 'forbidden zone'. To see how duality works, consider Maxwell's theory of electricity and magnetism, for example. Physicists have known for decades that if they interchange the electric field and magnetic field B in Maxwell's equations, and also swap the electric charge e and magnetic charge g, then the equations stay the same, That is, noyhing happens to Maxwell's theory if we make the dual transformation: E-B and e-g.
Hidden theories
In fact, in Maxwell's theory, the product e tinies g is a constant: so small e corresponds to large g. This is fhe key. Suppose an equation includes a mathematical function that depends on g^2 and which cannot be solved exactly. The standard mathematical trick is to approximate a solution with a perturbation expansion g^2 - g^4 - g^6 and go on - So long as g is less than 1. each successive term in the series is smaller than the last, and the overall value, converges on a single figure. But if g is greater than 1 then the total gets larger and larger, and the approximation fails, This is where duality comes in. If g is large, then e is less than 1. Using perturbation, we get the series e^2 + e^4 + e^6 which gives a sensible value. Ultimately, this means that using perturbation on e can solve problems in the non-perturbative region of g. Duality in Maxwell's theory is rather trivial. But in M-theory, we find another duality: g-1/g. 'This relationsbip, alhough simpler, turns out to be incredibly powerful, When I first saw it, I, could hardly believe my eyes. lt meant thit a string theory defined for large g, which is usually impossible to describe using present-day mathematics, can be shown to be equivalent to another type of string theory for small g, which is easily deicribed using perturbation theory. Thus, two different string theories can be dual to each other. In the non-perturbative region of string theory was another string theory! This is how in fact, we prove the equivalence of all five string theories. Altogether, three different types of duality called S, T and U have been discovered, which yield an intricate web of dualities linking string theories of various dimensions and types. At an incredible pace, physicists have now mapped almost all the tiolutions and dualities that exist in 10, 8 and 6 dimensions.
Before M-theory, finding the non.perturbative solutions in these dimensions would have been considered impossible. Now the problem is trivial. For example, let us say that two theories A and B are dual to each, other in 10 dimensions. If we compactify both theories in the same way, then we obtain then we obtain theories A' and B'. But now we know something new: that A' is also dual to B', Thus the non-perturbative bahaviour of of A' is given by B'. By elaborating this process, we get an almost complete understanding of the different possible universes down to 6 dimensions. Thus, M-theory solves entire classes of problem that were previously thought to be unsolvable, it even gives us valuable new details about quantum effects in black holes, But there are many loose ends. For example, what precisely is M-theory? So far, we. only know fragments of the theory, (the low-energy part). We are still waiting for someone to come up with a full description of M-theory. Last year, Vafa shocked Physicists by announcing that there may be a 12-dimensional theory out there, which he called f-theory, f for father.
More important, we are still far from mapping all the dualities of four dimensions. If everything works out as hoped, we should find out that one of these four-dimensional theories contains the strandard modeland thus describes the known universe,but there are millions of these solutions, so sifting through them to find the one we are after may take many years.
So this means that the end is in sight that some day we will be able to work out the Standard Model from first principles? When I put this question to some leading physicists in this field they were still cautious.
Here comes hypertime New Scentist 1 Nov 97
Yet despite its great promise, M-theory has not ironed out all the differences between the various string theories, which is where Vifa and his "F-theory" comes in, upping the ante to 12 dimensions.
the remaining problems began to fall away with an extra dimension, and tileoris@s eagerly welcomed Vafii's eqliatioiis. But tlie new dimension was one of time, and the philosophicAl implications are rather more troubling. "Most theorists would shun the idea of more than one time," says Duff, who is himself dabbled with the idea of a 12th time-like dimension. "it brings all sorts of headaches that we would rather do without." It's easy to see why. If time is like a striaght line, every point is either before or after every other point. Future and past are well defined. Every set of events has a unique sequence. But add another dimension and the line becomes a plane. How do you define future and past now? How do you link events-the whole game of physics-when the idea of effect following cause has evaporated? According to Duff that's not the end of it. Time dimensions differ fundamentally from space dimensions in one important respect: when you insert time into your equations it tends to come in with a negative rather than a positive sign. If you start to mess around with extra time dimensions, all sorts of -nasties start to emerge-objects that travel faster than light,' photons with negative energy, events where the probabilities of all possible outcomes don't add up to one.
Primitive tools
Admittedly, says Duff, the tools we use to under stand the world may be at fault. Perhaps the existing approaches are too primitive to describe multiple times. But since these are the only tools around, the best approach seems to be to treat Vafa's extra time dimension as a convenient device rather than a real physical entity. Exploit the benefits it offers and finesse your way around the disadvantages. Indeed, Vafa's new time has some suspicious characteristics that could justify this approacli. For instance, while the 11 dimensions of M-theory obey Einstein's relativity principle, which says that tile laws of physics should look the same to all observers, Vafa's 12 dimensions do not. This is one more reason for physicists to discount the new dimeiision's physical reality. "It's by no means on the same footing as ordinary time," says Frank Wilczek of the Institute for Advanced Study. Duff agrees. Though it looks like time in some limited ways, he says, "it's not a real, honest-to-goodness extra time dimension." Vafa admits that his extra dimension has many of the hallmarks of an abstract mathematical device rather than a real physical entity. But this may not be the case for much longer. "At this point, it's making the formalism took nicer," he says. "Whenever that happens in the history of physics, there's usually something behind it." Take quarks. A few decades ago, quarks were a mathematical construction-a way of thinking about the make-up of particles such as protons. According to the equations, quarks could never exist as single individuals. They seemed to be theoretical conveniences. Now, says Vafa, most physicists agree that quarks do exist in the physical world. The same happy fate could await his mysterious extra time dimension. But if it's really out there, why haven't we seen it? One possibility is that, along with the seven "missing" space dimensions, the extra time dimension is curled up so tightly that it's invisible to us. If so, the only way to unwrap it would be to focus huge amounts of energy into a tiny volume. This would have remarkable consequences. "If the [extra] time dimension could be unleashed, objects would not have the sensation of moving in time the way that we do," says Vafa. Think about it. In space we have choices about how to move, forwards and baakwards, up and down, left and right. For time, our only choice appears to be forward into the future-Hobson's choice. But with more than one time dimension, savs Wilczek, it might become possible to manoeuvre sideways in time, or diagonally. If we saw an undesirable event looming in the "future" we might even be able to sidestep it. Perhaps it's just as well, then, that the prospects of releasing Vafa's hidden dimension are actually rather remote. It is extremely unlikely that an energy intense enough to activate the missing time exists anywhere in our Universe though some physicists speculate that it might happen in the centre of a black hole. But that's not the end of the line for real life multiple times. After all, according to tlie latest cosmological theories there could be plenty of other universes, each of which might have its own unique combination of space and time dimensions. What would it be like in a truly multi-time universe? "It would really be a mindstretcher," says Wilczek. "Is it impossible? No I don't think so. You can write down the equations, but I have very little feeling for what the solutions would be like to live in."
 Prime Mover
New Scientist 8 Aug 98 18
Prime Mover
New Scientist 8 Aug 98 18
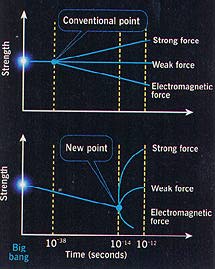
EARLY next century, we may be able to witness the single force that acted in the early Universe. A particle accelerator under construction at CERN, the European Laboratory for Particle Physics near Geneva, may have just enough energy to re-create the force, say physicists. In the earliest moments after the big bang, particles whizzed around with enormous energies. According to the so-called Grand Unified Theory, the three non-gravitational forces of nature-electromagnetic, weak and strong-acted as one at this time. But as the Universe cooled they split into the distinct forces we know today. Physicists believed the forces split when the particles' energies dropped to about 10^16 giga-electronvolts (GeV)-100 trillion times higher than is achievable in today's particle accelerators. This happened a mere 10^-18 seconds after the Universe formed. But now physicists Keith Dienes, Emilian Dudas and Tony Gherghetta of CERN have calculated that the forces could have 2 remained unified longer, down to energies of 1000 GeV That energy is within the reach of the CERN's Large Hadron Collider due to be completed in 2005. The physicists came to this conclusion after making calculations about the extra dimensions that the Universe may contain. Theorists believe we do not see these extra dimensions because they are tightly "rolled up" to around 10^-11 metres, a size that allows their effects to be felt only at the high energies that existed around the time of the big bang. If they were any bigger, there could be serious problems for the unified theory. It has been shown before that a host of new particles would rattle around in the extra dimensions, and bring with them more forces. "People thought the extra particles would make the forces too strong at the unification energy to be handled by current mathematical techniques," says Dienes. But Dienes and his team have calculated that a larger fifth dimension of about 10-19 metres would not cause this problem. The calculations also suggest that although the three non-gravitational forces would strengthen quickly as the energy rises, they would also converge at a lower energy than expected, long before the mathematics becomes too difficult to handle. Dienes's team has submitted papers on the work to Physics Letters B and Nuclear Physics B. The consequences of a much lower unification energy would be enormous. "All physics assumes unification occurs at an energy so high that it has no direct effect on the familiar world," says Gherghetta. "If it occurs at a lower energy, it would change everything, including our picture of the evolution of the Universe from the big bang." Marcus Chown