 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes live video seminars, enchanting renewal songs and a thousand page illustrated codex.
 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes
live video seminars, enchanting renewal songs and a thousand page
illustrated codex.
 Return
to Genesis of Eden?
Return
to Genesis of Eden?

STATIONARY STATES or wave patterns, associated with the energy
levels of a Rydberg atom (a highly excited hydrogen atom) in a strong magnetic
field can exhibit chaotic qualities. The states shown in the left two images
seem regular, the right two are chaotic. In the third picture the state
lies mostly along a periodic orbit; in the fourth, it does not and is difficult
to interpret, except for the four mirror symmetries with respect to the
vertical horizontal and two diagonal lines.
Quantum Chaos
Martin Gutzwiller Scientific American Jan 92
In 1917 Albert Einstein wrote a paper that was completely ignored for 40 years. In it he raised a question that physicists have only, recently begun asking themseves: What would classical chaos, which lurks everywhere in our work do to quantum mechanics. the theory describing the atomic and subatomic worlds? The effects of claccical chaos, of course, have long been observed-Kepler knew about the motion of the moon around the earth. and Newton complained bitterly about the phenomenon. At the end of the 19th century the American astronomer William Hill demonstrated that the irregularity is the reswt entirelly of the gravitational pull of the sun. So thereafter, the great French mathematician-astronomer-physicist Henri Poincare surmised that the moon's motion is only mild case of a congenital disease affecting nearlly everything. In the long run Poincare realized, most dynamic systems show no discernible regularity or repetitive pattern. The behavior of even a simple system can depend so sensitively on its initial conditions that the final outcome is uncertain. At about the time of Poincare's seminal work on classical chaos, Max Planck started another revolution, which would lead to the modern theory of quantum mechanics. The simple systems that Newton had studied were investigated again, but this time on the atomic scale. The quantum analogue of the humble pendulum is the laser; the flying cannonballs of the atomic world consist of beams of protons or electrons, and the rotating wheel is the spinning electron (the basis of magnetic tapes). Even the solar system itself is mirrored in each of the atoms found in the periodic table of the elements. Perhaps the single most outstanding feature of the quantum world is its smooth and wavelike nature. This feature leids to the question of how chaos makes itself felt when moving from the classical world to the quantum world. How can the extremelly irregular character of classical chaos be reconciled with the smooth and wavelike nature of phenomena on the atomic scale? Does chaos exist in the quantum world'? Preliminary work seems to show that it does. Chaos is found in the distribution of energy levels of certain atomic systems; it even appears to sneak into the wave patterns associated with those levels. Chaos is also found when electrons scatter from small molecules. I must emphasize, however, that the term 'quantum chaos' serves more to describe a conundrum than to define a well-posed problem.
Considering the following interpretation of the bigger picture may be helpful in coming to grips with quantum chaos. All our theoretical discussions of mechanics can be somewhat artificially divided into three compartments [see illustration ] although nature recognizes none of these divisions. Elementary classical mechanics falls in the first compartment. This box contains all the nice, clean systems exhibiting simple and regular behavior, and so I shall call it R, for regular. .Also contained in R is an elaborate mathematical tool called perturbation theory which is used to calculate the effects of small interactions and extraneous disturbances, such as the influence of the sun on the moon's motion around the earth. With the help of perturbation theory, a large part of physics is understood nowadays as making relatively mild modifications of regular systems. Reality though, is much more complicated; chaotic systems lie outside the range of perturbation theory and they constitute the second compartment. Since the first detailed analyses of the systems of the second compartment were done by Poincare, I shall name this box P in his honor. It is stuffed with the chaotic dynamic systems that are the bread and butter of science. Among these systems are all the fundamental problems of mechanics, starting with three, rather than only two bodies interacting with one another, such as the earth, moon and sun, or the three atoms in the water molecule, or the three quarks in the proton. Quantum mechanics, as it has been practiced for about 90 years, belongs in the third compartment, caned Q. After the pioneering work of Planck, Einstein and Niels Bohr. quantum mechanics was given its deftnitive form in four short years, starting in 1924. The seminal work of Louis de Brogbe, Werner Heisenberg, Erwin Schrodinger, Max Born, Wolfgang Pauli and Paul Dirac has stood the test of the laboratory without the slightest lapse. Miraculously. it provides physics with a matheniatical framework that, according to Dirac, has yielded a deep understanding of 'most of phlsics and all of chemistry" Nevertheless, even though most physicists and chemists have learned how to solve special probleins in quantum mechanics, they have yet to come to terms with the incredible subtleties of the field. These subtleties are quite separate from the difficult, conceptual issues having to do with the interpretation of quantum mechanics. The three boxes R (classic, simple sytems), P (classic chaotic systems) and Q (quantum systems) are linked by several connections. The connection between R and Q is known as Bohr's correspondence principle. The correspondence principle claims, quite reasonably, that classical mechanics must be contained in quantum mechanics in the limit where objects become much larger than the size of atoms- The main connection between R and P is the Kolmogorov- Arnold-.Moser (KAM) theorem. The KAM theorem provides a powerful tool for calculating how much of the structure of a regular system survives when a small perturbation is introduced, and the theorem can thus identify perturbations that cause a regular system to undergo chaotic behaviour. Quantum chaos is concerned with establishing the relation between boxes P (chaotic systems and Q (quantum systems). In establishing this relation, it is useful to introduce a concept called phase space. Quite amazingly this concept, which is now so widely exploited by experts in the field of dynamic systems, dates back to Newton. The notion of phase space can be found in Newton's mathematical Principles of Natural Philosophy published in 1687. In the second definition of the first chapter, entitled 'Definitions," Newton states (as translated from the original Latin in 1729): The quantity of motion is the measure of the same, arising from the velocity and quantity of matter conjointly" In modern English this means that for every object there is a quantity. called momentum, which is the product of the mass and velocity of the object. Newton gives his laws of motion in the second chapter, entitled 'Axioms, or Laws of motion.' The second law says that the change of motion is proprotional to the motive force impressed. Newton relates the force to the change of momentum (not to the acceleration as most textbooks do).
Momentum is actually one of two quantities that, taken together, yield the complete information about a dynamic system at any instant The other quantity is simply position. which determines the strength and direction of the force. Newton's insight into the dual nature of momentum and position was put on firmer ground some 130 years later by two mathematicians, William Rowan Hamilton and Karl Gustav- Jacob Jacobi. The pairing of momentum and position is no longer viewed in the good old Euclidean space or three dimensions; instead it is viewed in phase space, which has six dimensions, three dimensions for position and three for momentum The introduction of phase space was a powerful step from a mathematical point of view, but it represents a serious setback from the standpoint of human intuition. Who can visualize six dimensions?',' In some cases fortunately phase space can be reduced to three or even better, two dimensions. Such a reduction is possible in examining the behaxior of a hydrogen atom in a strong magnetic field. The hydrogen atom has long been a highily desirable system because of its simplicity. A lone electron moves around a lone proton. And yet the classical motion of the electron becomes chaotic when the magnetic field is turned on. How can we claim to understand physics if we cannot explain this basic problem?

POINCARE SECTION OF A HYDROGEN ATOM in a strong magnetic field
has regions where
the points of the electron's trajectory scatter wildly, indicating chaotic
behavior. The section
is a slice out of phase space, an abstract six-dimensional space: the usual
three for the
position of a particle and an additional three for the particle's momentum.
Under normal conditions, the electron of a hydrogen atom is tightly bound to the proton. The behavior of the atom is governed by quantum mechanics. The atom is not free to take on any arbitrary energy, it can take on only discrete, or quantized, energies. At low energies, the allowed values are spread relatively far apart. As the eneri,,)- of the atom is increased, the atom grows bigger, because the electron moves farther from the proton, and the allowed energies get closer together. At high enough energies (but not too high. or the atom will be stripped of its electron!), the allowed energies get very close together into what is effectively a continuum, and it now, becomes fair to apply the rules of classical mechanics. Such a highly excited atom is called a Rydberg atom. Rydberg atoms inhabit the middle ground between the quantum and the classical worlds, and they are therefore ideal candidates for exploring Bohr's correspondence principle which connects boxes Q (quantum phenomena) and R (classic phenomenal. If a Rydberg atom could be made to exhibit chaotic behavior in the classical sense, it might provide a clue as to the nature of quantum chaos and thereby shed light on the middle ground between boxes Q and P (chaotic phenomena. A Rdberg atom exhibits chaotic behaviour in a strong magnetic field, but to see this behavior we must reduce the dimension of the phase space. 'The first step is to note that the applied magnetic field defines an axis of symmetry through the atom. The motion of the electron takes place effectively in a two-dimensional plane, and the motion around the axis can be separated out; ornly the distances along the axis and from the axis matter. The symmetty of motion reduces the dimension of the phase space from six to four. Additional help comes from the fact that no outside force does any work on the electron. As a consequence, the total energy does not change with time. By focusing attention on a particular value of the energy, one can take a three-dimensional slice-called an energy shell-out of the four-dimensional phase space. The energy shell allows one to watch the twists and turns of the electron, and one can actually see something resembling a tangled wire sculpture. The resulting picture can be simplffied even further through a simple idea that occurred to Poincare. He suggested taking a fixed two-dimensional plane (called a Poincare section, or a surface of section) through the energy shell and watching the points at which the trajectory intersects the surface. The Poincare section reduces the tangled wire scwpture to a sequence of points in an ordinary plane. A Poincare section for a highly excited hydrogen atom in a strong magnetic field is shown on the opposite page. The regions of the phase space where the points are badly scattered indicate chaotic behavior. Such scattering is a clear symptom of classical chaos, and it aflows one to separate systems into either box P or box R.
What does the Rydberg atom reveal about the relation between boxes P and Q? I have mentioned that one of the trademarks of a quantum mechanical system is its quantized energy levels, and in fact the energy levels are the first place to look for quantum chaos. Chaos does not make itself felt at any particular energy level, however; rather its presence is seen in the spectrum, or distribution, of the levels. Perhaps somewhat paradoxically in a nonchaotic quantum system the energy levels are distributed randomly and without correlation, whereas the energy levels of a chaotic quantum system exhibit strong correlations [see illustration] The levels of the regular system are often close to one another, because a regular system is composed of smaller subsystems that are completely decoupled. The energy levels of the chaotic system, however, almost seem to be aware of one another and try to keep a safe distance. A chaotic sytem cannot be decomposed; the motion along one coordinate axis is always coupled to what happens along the other axis.
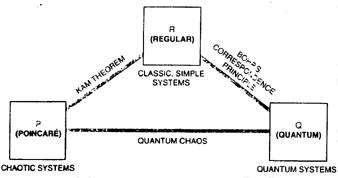
MECHANICS is traditionally (and artificially) divided into
the three compartments depicted here,
which are linked together by several connections. Quantum chaos is concerned
with establishing the relation between boxes P and Q.
The spectrum of a chaotic quantum system was first suggested by Eugene P. Wigner, another early master of quantum mechanics. Wigner observed, as had many others, that nuclear physics does not possess the safe underpinnings of atomic and molecular physics: the origin of the nuclear force is still not clearly understood. He therefore asked whether the statistical properties of nuclear spectra could be derived from the assumption that many parameters in the problem have definite, but unknown values. This rather vague starting point allowed him to find the most probable formula for the distribution. Oriol Bohigas and Marie-Joya Giannoni of the Institute of Nuclear Physics in Orsay France, first pointed out that Wigner's distribution happens io be exactly what is found for the spectrum of a chaotic dynamic system.
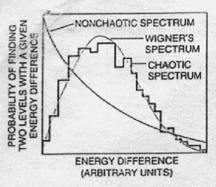
ENERGY SPECTRUM or distribution of energy levels, differs
markedly between chaotic and
nonchaotic quantum systems. For a nonchaotic system such as a molecular
hydrogen ion (H2+),
the probability of finding two energy levels close to each other is quite
Wgh. In the case of a
chaotic system such as a Rydberg atom in a strong magnetic field, the probability
is low. The chaotic
spectrum closely matches the typical nuclear spectrum derived many years
ago by Eugene P. Wigner.
Chaos does not seem to limit itself to the distribution of quantum energy levels, however, it even appears to work its way into the wavelike nature of the quantm world. The position of the electron in the hydrogen atom is described by a wave pattern. The electron cannot be pinpointed in space; it is a cloudlike smear hovering near the proton. Associated with each allowed energy level is a stationary state, which is a wave pattern that does not change with time. A stationary state corresponds quite closely to the vibrational pattemrn of a membrane that is stretched over a rigid frame, such as a drum. The stationary states of a chaotic system have surprisingly interesting structure, as demonstrated in the early 1980s by Eric Heller of the University of Washington. He and his students calculated a series of stationary states for a two-dimensional cavity in the shape of a stadium. The corresponding problem in classical mechanics was known to be chaotic, for a typical trajectory quickly covers most of the avai;able ground quite evenly. Such behavior suggests that the stationary states might also look random, as if they had been designed without rhyme or reason. In contrast. Heller discovered that most stationary states are concentrated around narrow channels that form simple shapes inside the stadium, and he called these channels "scars" [see illustration]. Similar structure can also be found in the stationery states of a hydrogen atom in a strong magnetic field [see illustration] The smoothness of the quantum wave forms is preserved from point to point, but when one steps back to view the whole picture, the fingerprint of chaos emerges. It is possible to connect the chaotic signature of the energy spectrum to ordinary classical mechanics. A clue to the prescription is provided in Einstein's 1917 paper, He examined the phase space of a regular system from box R and described it geometrically as filled with surfaces in the shape of a donut; the motion of the system corresponds to the trajectory of a point over the surface of a particular donut. The trajectory winds its way around the surface of the donut in a regular manner, but it does not necessarily close on itself. In Einstein's picture, the application of Bohr's correspondeice principle to find the energy levels of the analogous quantum mechanical system is simple. The only trajectories that can occur in nature are those in which the cross section of the donut encloses an area equal to an integral multiple of Planck's constant, h (2pi times the fundamental quantum of angular momentum having the units of momentum multiplied by length). It tums out that the integral multiple is precisely the number that specifies the corresponding energy level in the quantum system Unfortimately as Einstein clearly saw, his method cannot be applied if the system is chaotic, for the trajectory does not lie on a donut and there is no natural area to enclose an integral multiple of Planck's constant. A new approach must be sought to explain the distribution of quantum mechanical energy levels in terms of the chaotic orbits of classical mechanics. Which features of the trajectory of classical mechanics help us to understand quantum chaos? Hill's discussion of the moon's irregular orbit because of the presence of the sun provides a clue. His work represented the first instance where a particular periodic orbit is found to be at the bottom of a difficult mechanical problem. (A periodic orbit is tike a closed track on which the system is made to run: there are many of them, although they are isolated and unstable.) Inspiration can also be drawn from Poincare, who emphasized the general importance of periodic orbits. In the begining of his three-volume work-, The New Methods of Celestial Mechanics" which appeared in 1892, he expresses the belief that periodic orbits 'offer the only opening through which we might penetrate into the fortress that has the reputation of being impregnable." Phase space for a chaotic system can be organized, at least partially around periodic orbits, even though they are sometimes quite difficult to find.
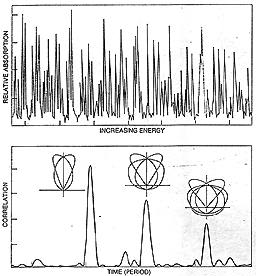
ABSORPTION OF LIGHT by a hydrogen atom in a strong magnetic
field appears to vary randomly
as a function of energy (top), but when the data are anallzed according
to the mathematical procedure
called Fourier analysis, a distinct pattern emerges (bottom). Each peak
in the bottom panel
has associated with it a specific classical periodic orbit.
In 1970 I discovered a very general way to extract information about the quantum mechanical spectrum from a complete enumeration of the classical periodic orbits. The mathematics of the approach is too difficult to delve into here, but the main result of the method is a relatively simple expression called a trace formula. The approach has now been used by a number of investigators, including Michael V. Berry of the University of Bristol, who has used the formula to derive the statistical properties of the spectrum. I have applied the trace formula to compute the lowest two dozen energy levels for an electron in a semiconductor lattice, near one of the carefully controlled impurities. (the serriicondoctor, of course, is the basis of the marvellous devices on which modern life depends; because of its impurities, the electrical conductivity of the material is half-way between that of an insulator, such as plastic, and that of a conductor, such as copper.) The trajectory of the electron can be uniquely characterized by a string of symbols, which has a straightforward interpretation. The string is produced by defining an axis through the semiconductor and simply noting when the trajectory crosses the axis. A crossing to the "positive" side of the axis gets the symbol +, and a crossing to the 'negative" side gets the symbol -. A trajectory then looks exactly like the record of a coin toss. Even if the past is known in all detail even if all the crossings have been recorded-the future is still wide open. The sequence of crossings can be chosen arbitrarily. Now, a periodic orbit consists of a binary sequence that repeats itself; the simplest such sequence is (+ -), the next is (+ -), and so on (Two crossings in a row having the same sign indicate that the electron has been trapped temporarily.) All periodic orbits are thereby enumerated, and it is possible to calculate an appropriate spectrum with the help of the trace formula. In other words, the quantum mechanical energy levels are obtained in an approximation that relies on quantities from classical mechanics only. The dassical periodic orbits and the quantum mechanical spectrum are closely bound together through the mathematical process called Fourier analyis. The hidden regularities in one set, and the frequencies with which they show up, are exactly given by the other set. This idea was used by John B. Delos of the College of William and Mary and Dieter Wintgen of the Niax Planck Institute for Nuclear Physics in Heidelberg to interpret the spectrum of the hydrogen atom m a strong magnetic field. Experimental work on such spectra has been done by Karl H. Welge and his colleagues at the University of Bielefeld, who have excited hydrogen atoms nearly to the point of ionization where the electron tears itself free of the proton. The energies at which the atoms absorb radiation appear to be quite random [see illustration], but a Fourier analysis converts the jumble of peaks into a set of well-separated peaks. The important feature here is that each of the well-separated peaks corresponds precisely to one of several standard classical periodic orbits. Poincare's insistence on the iinportance of periodic orbits now takes on a new meaning. Not only does the classical organization of phase space depend critically on the classical periodic orbits, but so too does the understanding of a chaotic quantum spectrum.
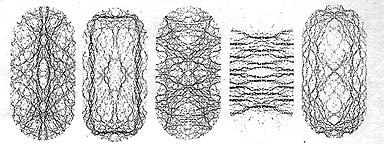
PARTICLE IN A STADIUM-SHAPED BOX has chaotic stationary states
with associated
wave patterns that look less random than one might expect. Most of the states
are
concentrated around narrow channels that form simple shapes, called scars.
So far I have talked only about quantum systems in which an S electron is trapped or spatially confined. Chaotic effects are also present in atomic systems where an electron can roam freelly, as it does when it is scattered from the atoms in a molecule. Here energy is no longer quantized, and the electron can take on any value, but the effectiveness of the scattering depends on the energy. Chaos shows up in quantum scattering as variations in the amount of time the electron is temporarily caught inside the molecule during the scattering process. For simplicity the problem can be eexamined in two dimensions. To the electron, a molecule consisting of four atoms looks like a small maze. When the electron approaches one of the atoms, it has two choices: it can turn left or right. Each possible trajectory of the electron through the molecule can be recorded as a series of left and right turns around the atom. until the particle finally emerges. All of the trajectories are unstable: even a minute change in the energy or the initial direction of the approach will cause a large change in the direction in which the electron eventually leaves molecule. The chaos in the scattering process comes from the fact that the number of trajectories increases rapidly with path length. Only an interpretation From the quantum mechanical point of view gives reasonable results; a purely classical calculation yields nonsensical results. In quantum mechanics each classical trajectory is used to deftne a little wavelet that finds its way through the molecule. The quantum mechanical result follows from simply adding up all such wavelets. Recently I have done a calculation of the scattering process for a special case in which the sum of the wavelets is exact An electron of known momentum hits a and emerges with the same momentum The arriarrival time for the electron to reach a fixed monitoring station varies as a function of the momentum and the way in which it varies is so fascinating about this problem. The arrival time fluctuates over small changes in the momentum but over large changes a chotic imprint emerges which never settles down to any simple pattern [see illustration].
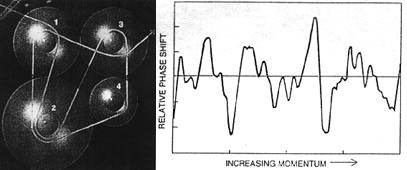 TRAJECTORY OIF AN ELECTRON through a molecule
during scattering can be recorded as a series of
TRAJECTORY OIF AN ELECTRON through a molecule
during scattering can be recorded as a series of
left and right turns ,around the atoms making up the molecule (left). Chaotic
variation (right)
characterizes the time it takes for a scattered electron of known momentum
to reach a fixed monitoring
station. Arrival time varies as a function of the electron's momentum. The
variation is smooth when
changes in the momentum are small but exhibits a complex chaotic pattern
when the changes are large.
The quantity-shown on the vertical axis the phase shift, is a measure of
the time delay.
A particularly tantalizing aspect of the chaotic scattering process is that it may connect the mysteries of quantum chaos with the mysteries of number theory. The calculation of the time delay leads straight into what is probably the most enigmatic object in mathematics, Riemann's zeta function. Actually it was first emploed by Leonhard Euler in the middle of the 18th century to show the existence of an infinite number of prime numbers (integers that cannot be divided by any smaller integer other than one). About a century later Bernhard Riemann, one of the founders of modem mathematics, employed the function to delve into the distribution of the primes. in his only paper on the subject, he called the function by the Greek letter zeta. The zeta function is a function of two variables, x and y which exist in the complex plane). To understand the distribution of prime numbers, Riemann needed to know when the zeta function has the value of zero. W'ithout giving a valid argument, he stated that it is zero only when x is set equal to 1/2. Vast calculations have shown that he was right without exception for the first billion zeros, but no mathematician has come even close to providing a proof. If Riemann's conjecture is corrcct, all kinds of interesting properties of prime numbers could be proved. The values of y for which the zeta function is zero form a set of numbers that is much like the spectrum of energies of an atom. Just as one can study the distribution of energy levels in the spectrum so can one study the distribution of zeros for the zeta function. Here the prime numbers play the same role as the classical closed orbits of the hydrogen atom in a magnetic field: the primes indicate some of the hidden correlations among the zeros of the zeta function. In the scattering problem the zeros of the zeta function give the values of the momentum where the time delay changes strongly. The chaos of the Riemann zeta function is particularly apparent in a theorem that has only recently been proved: the zeta function fits locally any smooth function. The theorem suggests that the function maydescribe all the chaotic behavior a quantum system can exhibit. If the mathematics of quantum mechanics could be handled more skilfully, many examples of locally smooth, yet globally chaotic, phenomena might be found.

Chaotic (magenta) and periodic (cyan) trajectories of an electron
through a crystal lattice are contrasted over
the wave functions of the lattice (the atoms are the dark ovals). In quantum-confined
systems the chaotic
trajectories may be eventually quasi-periodic i.e. chaotic orbits may over
time become trapped in periodic
solutions. Once we release the confinement of the electron, either to a
single wave function or to an ordered
crystal, as is the case in kinetic interactions in a non-crystalline molecular
medium, this quantum break time
to periodicity may never become realized explaining the perseverence of
chaotic orbits.
Where Two Worlds Meet Julian Brown New Scientist 16 May 96
TWICE in 20th-century physics, the notion of unpredictability has shaken scientists' view of the Universe. The first time was the development of quantum mechanics, the theory that describes the behaviour of matter on an atomic scale. The second came with the classical phenomenon of chaos In both areas unpredictable features changed scientists understanding of matter in ways that were totally unforeseen. How ironic then, that these two fields, which have something so fundamental in common, should end up as antagonists when combined. For by rights, chaos should not exist at all in quantum systems- the laws of quantum mechanics actually forbid it. Yet recent experiments seem to show the footprints of quantum chaos in remarkable swirling patterns of atomic disorder. These intriguing patterns could illuminate one of the darkest corners of modern physics: the twilight zone where the quantum and classical worlds meet. The quantum theory is one of the most successful theories in modern science.
Developed in the 1920s, it accounts for a vast range of phenomena from the nature of chemical bonds to the behaviour of subatomic particles, making predictions that have been tested to unprecedented levels of accuracy. But at its core there are troublesome features: Prominent among them is Heisenberg's uncertainty principle-if you know the speed of a quantum particle, for instance, you can never know its exact location. The notion that some aspects of nature are simply unknowable has caused sleepless nights for more than a few physicists. Chaos is a younger discipline. Although some of its conceptual elements had already been appreciated by Leibnitz in the 17th century and Poincare in the 19th century, chaos theory did not become fashionable until the 1980s when scientists began to realize that the phenomenon is widespread in the natural world. it arises when a system is unusually sensitive to its initial conditions so that a small perturbation of the system changes its subsequent behaviour in a way that grows exponentially with time. Chaos has been observed in, among other things, pendulums, the growth of populations, planetary dynamics, and weather systems. Probably the most famous example of chaos is the so-called "butterfly effect" in which, in theory, the tiny air disturbance from the flapping of a butterfly's wings can ultimately lead to a dramatic storm. of course, although both these theo.ries place fundamental limits on what we can know about/the world, the unpredictabilities in quantum theory and chaos are different in kind. But the particular problem with quantum chaos is that in quantum mechanics small perturbations generally only lead to small perturbations in subsequent states. Without the exponential divergence in evolutionary paths, it is difficult to see how there can be any chaos. This behaviour of quantum systems is often attreibuted to a special property of the quantlani equations: their linearity.
 Semi-classical description of the stadium illustrates
how a wavelet, unlike the classical trajectories begins to display periodic
behaviour as a result of the overlapping superposition of wavelets, which
unlike classical trajectories cannot densely fillphase space without overlapping.
Semi-classical description of the stadium illustrates
how a wavelet, unlike the classical trajectories begins to display periodic
behaviour as a result of the overlapping superposition of wavelets, which
unlike classical trajectories cannot densely fillphase space without overlapping.
An everyday example of linearity can be seen in a rubber band. When it is stretched a little the extension is proportional to the force. Nonlinearity steps in when you pull too far and the band reaches its limit of elasticity. Stretch even further and it snaps. Because nonlinearity is known to be a crucial ingredient in ch,iotic systems. it is often said that quantum mechanics cannot be chaotic
because it is linear. But according to Michael Berry, a leading theorist in the study of quantum chaos at the University of Bristol, this issue of linearity is a red herring. "This is one of the biggest misconceptions in the business he says. Berry's preferred explanation for the difference between what happens in classical and qtiaiitum systenis as they edge towards chaos is that quantum uncertainty iniposes a fundamental limit on the sharpness of the dynamics. The ammount of uncertainty is quantified in Heisenberg's uncertainty principle by a fixed value known as Planck's constantIn classical mechanics, objects can move along infinitely many trajectories," says Berry. This makes it easy to set up complicated dynamics in which an object will never retrace its path-the sort of beliaviour that leads to chaos. But in quantum mechanics, Planck's constant blurs out the fine detail, smoothing away the chaos."
This raises some interesting questions. What happens if you scale down a classically chaotic system to atomic size? Do you still get chaos or does quantum regularity suddenly prevail'? Or does someting entirely new happen? And why is it that macroscopic systems can be chaotic, given that ultimately everything is made out of atoms and therefore quantum in nature? These questions have been the subject of intense debate for more than a decade. But now a number of experimental approaches have begun to offer answers.
Scrambled spectra
One of the earliest clues came from investigations of atomic absorption spectra. If an atom absorbs a photon of light it is possible for one of its electrons to be kicked into a higher energy state. Normally, an atom's energy levels are spaced at mathematically regular intervals, accounted for by aii empirical formula given 19th cent physicist Johannes Rydberg. If an atom absorbs photons with different energies, electrons are kicked into different levels, and the result is a nice tidy absorbtion spectrum whose details are characteristic of the chemical element involved. But when the atom is subjected to a magnetic field the line structure of the spectrum becomes distorted. When the field is sufficiently intense the spectrum becomes so scrambled it looks pretty much random at higher energies. The phenomenon is easier to understand in classical rather than quantum mechanical terms. Viewed classically, atomic electrons movbe in orbits around the nucleus rather like planets round the Sun. A magnetic field, though, introduces an additional force which causes the electrons to swerve from their normal trajectories. It's rather like a stray star encroaching upon the Solar System. If it got sufficiently close the gravitational pull would at some point become comparable to the pull between the Earth and our sun. At this moment the earth would find itself in a tug-of-war between the sun and the interloping star. Such a system would very probably be unstable, with the Earth switching critically between orbits around the sun and the other star. The result would be a chaotic orbit. In the case of excited atoms, for small fields and lower energy states. The electromagnetic swerving is small compared with the electrostatic pull towards the nucleus and the electron continues to follow a stable orbit. But for strong fields and highly excited states where the electron is on average very much further away from the nucleus,the swerving force becomes comparable to the inward pull of the nucleus In this situation, according to vclassical predictions, the motion ought to be chaotic. The effect was first studied back in 1969 by two astronomers Garton and Tonkins of Imperial College, London, who wanted to find out how the spectra of stars would be affected by their powerful magnetic fields. Their experiments on barium atoms produced one of the first surprisesbecause their resulting spectrum still displayed considerable regularity. A grioup at the University of Bielefield in Germany repeated the experiments in the 1980s using higher resolution equipment. Although the randomness was more apparent in their spectra, it was still clear that quantum mechanics was in some strange way superimposing its own order on the chaos.
Quantum billiards
More recently, signs of quantum suppression of chaos have come from anotheianother experimental approach to quantum chaos: quantum billiards. OOn a conventional billiard table it is quite common for a player to pot a ball by bouncing the cue ball off the cushion first. In the hands of a skilled player, such shots are often quite repeatable. But if you were to try the saine shot on a rounded, stadium-shaped table, the results are far less predictible: the slightest change in starting position alters the ball's trajectory drastically. So what you get if you play stadium billiards is chaos. In 1992 at Boston's Northeastern University, Srinivas Sridhar and colleagues substituted microwaves for billiard balls and a shallow stadium-shaped copper cavity for the table. Sridhar's team then observed how the microwaves settled down inside the cavity. Although their apparatus is not of atomic proportions (a cavity typically measures several millimetres across the experiment exploits the precise similarity between the wave equations of quantum mechanics and the equations of the electromagnetic waves in this two-dimensional situation. If microwaves behaved like billiard balls, you would not expect to see any regular patterns. The experiments, however, reveal structures known its "scars" that suggest the waves concentrate along particular paths. But where do these paths come from? One answer is provided by theoretical work carried out back in the 1970s by Martin Gutzwiller of of the IBM Thomas Watson Center in Yorktown Heights near New York. He produced a key formula that showed how classical chaos might relate to quantum chaos. Basically it indicates that the quantum regularities are related to a very limited range of classical orbits. These orbits are ones that are periodic in the classical system. If, for example, you placed a ball on the stadium table and hit it along exactly the right path, you could get it to retrace its path after only a few bounces off the cushions. however, because the system is chaotic these orbits are unstable. You only need a minuscule error and the ball will move off course within a few bounces. So classically you would not expect to see these orbits stand out. But thanks to the uncertainty in quantum mechanics, which "frizzes" the trajectories of the balls, tiny errors become less significant and the periodic orbits are reinforced in some strange way so that they predominate. Sridhar's millimetre-sized stadium was a good analogy for quantum behaviour, but would the same effects occur in a truly quantum-sized system? This question was answered recently by Laurence Eaves from the University of Nottingham, and his colleagues at Nottingham and at Tokyo University. Eaves conducted his game of quantum billiards inside an elaborate semiconductor "sandwich". He used electrons for balls, and for cushions he used a combination of quantum barriers and magnetic fields. The quantum barriers are formed by the outer layers of the sandwich, which gives the electrons a couple of straight edges to bounce back and forth between, The other edges of the table are created by the restraining effect of the magnetic field, which curves the electron motion in a complicated way. As in Sridhar's stadium cavity, the resulting dynamics ought to be chaotic.
Number crunching
To do the exeriments, Eaves needed ultra-intense magnetic fields, so he took his device to the High Magnetic Field Laboratory at the University of Tokyo, which is equipped with some of the most powerful sources of pulsed magnetic fields in the world. Meanwhile his colleagues in Noitingham, Paul Wilkinson, Mark Fromhold and Fred Sheard, squared up to a heroic series of calculations, deducing from purely quantum mechanical principles what the results should look like. In a spectacular pape that made the cover of Nature last month, the team produced the first definitive evidence for quantum scarring, and precisely confirmed the quantum mechanical predictions. Sure enough, the current flowing through the device was predominantly carried by electrons moving in certain 'scarred' paths. Quantum regularity was lingering in the chaos rather like the smile of the Cheshire cat in Alice's adventures in wonderland.
In case these ideas seem academic it is worth noting that quantum chaos could play an important role in the design of future seniiconductor devices. At the moment, transistor devices on silicon chips are still large enough for the electrons to move through them diffusively like molecules in a gas. But as chip manufacturers squeeze ever more logic gates onto silicon, says Eaves, in the next is years transistors may become so small that electrons will instead flow through them more like quantum billiard balls. "At this point, we may well need the principles of quantum chaos to understand how these devices will work," lie says. But where does that leave the problem of how quantum mechanics turns into the classical world on larger scales? One way of looking at the problem is to investigzite how a quantum chaos system actually evolves with time. Last December, Mark Raizen and his colleagues at. the University of Texas managed to do just that, using an experimental version of a quantum kicked rotor. The idea is to couple two oscillating systems to produce chaos. Imagine pushing a child's swing. If you time your pushes in rhythm with
the swing, then it simply rises higher and higher. if you push at a different frequency, the swing will sometimes be given a boost and sometimes slowed down. if this is done too vigorously, the oscillations become chaotic. In Raizen's quantum version, ultra-cold sodium atoms were subjected to a special kind of pulsed laser light. The laser beam was bounced between mirrors to set up a short-lived standing wave-a periodic lattice of light that remains motionless in space rather like the acoustic nodes on a violin string. Depending on their precise location in the standing waves, the sodium atoms are pushed around by the magnetic fields in the lattice. According to classical calculations, the result is that the atoms should be kicked chaotically along an increasingly energetic random walk. Raizen's results confirmed a long- standing prediction of the quantum theoretical descriptions of these systems. The atoms did indeed move in a chaotic way to begin with. But after around 100 microseconds (which corresponds to around 50 kicks) the build-up in energy reached a plateau.
Break time
In other words. quantum mechanics does suppress the chaos but only after a certain amount of time known as the 'quantum break time'. This turns out to be the crucial feature that distinguishes between quantum and classical predictions of chaotic systems. Before the break time, quantum systems are able to mimic the behaviour of classical systems by looking essentially random. But after the break time, the system simply retraces its path. it is no longer random, but akin to a repeating loop, albeit of considerable complexity. But if this is right, how can classical systems exhibit chaos? Macroscopic objects such as pendulums and planets are, after all, made out of atoms and are therefore, ultimately, quantum systems. it turns out that classical systems are in fact behaving exactly like quantum systems. The only difference is that for classical systems, the quantum break times of macroscopic systems are extraordinarily long-far longer than the age of the Universe. if we could study a classical system for longer than its quantum break time, we would see that the behaviour was not chaotic but quasi-periodic instead. Thus, quantum and classical realities can be reconciled, with the classical world naturally embedded in a larger quantum reality. Or, as physicist Dan Kleppner of ttie Massachusetts Institute of Technology puts it, "Anything classical mechanics can do, quantum mechanics can do better". Since much of the experimental work on quantum chaos has agreed with theoretical predictions, it could be tempting to say "So what?". We already knew that quantum theory was right. Well, research on quantum chaos does hold out the promise of some remarkable discoveries. Berry is excited by what appears to be a deep connection between the problem of finding the energy levels of a quantum system that is classically chaotic and one of the biggest unsolved mysteries in mathematics: the Riemann hypothesis. This concerns the distribution of prime numbers. if you choose a number n and ask how many prime numbers there are less than n it turns out that the answer closely approximates the formula: n/log n. The formula is not exact, though: sometimes it is a little high and sometimes it is a little low. Riemann looked at these deviations and saw that they contained periodicities. Berry likens these to musical harmonies: "The question is what are the harmonies in the music of the primes? Amazingly, these harmonies or magic numbers behave exactly like the energy levels in quantum systems that classically would be chaotic."
Deep connection
This correspondence emerges from statistical correlations between the spacing of the Riemann numbers and the spacing of the energy levels. Berry and his collaborator Jon Keating used them to show how techniques in number theory can be applied to problems in quantum chaos and vice versa. In itself such a connection is very tintisual- Although sonictimes described as the Queen of mathematics, number theory is often thought of as pretty useless, so this deep connection with physics is quite astonishing. Berry is also convinced that there must be a particular chaotic system which when quantised would have energy levels that exactly duplicate the Riemann numbers. 'Finding this system could be the discovery of the century," he says. it would become a model system for describing chaotic systems in the same way that the simple harmonic oscillator is used as a model for all kinds of complicated oscillators. It could play a fundamental role in describing all kinds of chaos. The search for this model system could be the holy grail of chaos. Until we cannot be sure of its properties, but Berry believes the system is likely to be rather simple, and expects it to lead to totally new physics. It is a tantalising thought. out there is a physical structure waiting to be discovered. if we find it, the remarkablee experiments that we have recently witnessed in this discipline would be crowned by an experimental apparatus that could do more than anything to unlock the secrets of quantum chaos.
Chaotic Chaos Scientific American Mar 94.
Students of chaos have clung to the notion that chaotic systems retain some shreds of order. The shreds manifest themselves in the form of an attractor, a pattern of behavior toward which the system periodically settles. identifying the attractor enables one to predict the final behavior of a chaotic system, at least in a qualitative, statistical sense. That comforting notion has been damaged by Edward Ott of the University of Maryland and John C. Sommerer of Johns Hopkins University and their colleagues. They have shown that for certain systems that have more than one attractor, even qualitative predictions are impossible. "The repeatability of an experiment gets thrown into question," Ott says. The problem is rooted in the way a chaotic system determines which attractor to follow. The initial conditions that control the choice are said to be located in a basin of attraction. Ott and Sommerer have spoiled the party by showing that a basin may be rather leaky: it may have "holes" that make it impossible to predict which attractor the system will follow. Building on earlier mathematical work, the physicists used a computer to conduct numerical experiments in which a particle moving on a frictional surface is occasionally pushed. Consequently, the particle could begin moving either periodically or sporadically. The researchers found that even for this fairly simple system they could not determine which of the two attractors the particle would chase, because one basin is riddled with pieces of the other basin. in fact, every area in one basin, no matter how small, contained pieces of the other basin within it. "Hence, arbitrarily small changes can cause the system to go to a completely different attractor," Ott remarks. The only way to guarantee an outcome is not to have any error or noise whatsoever-a practical impossibility for real systems. And, anyway, what kind of chaos would that be? Ott points out that the results differ from other forms of chaos in which the starting point straddles the boundary between two basins of attraction. In such borderline situations, one might be able to move the starting point away from the boundary so that the attractor can be predicted. The same cannot be done for systems that have riddled basins, because no region is free of holes. "You're always on the borderline," Ott explains. Although riddled basins appear only in situations that have certain spatial symmetries, they are probably not rare. "A lot of physics is based on conservation laws, which are based on symmetries," Sommerer observes. Currently the workers are looking for real physical phenomena that have riddled basins. They suspect that turbulent fluids, chemical mixtures and lasers may be among such systems. Sommerer even speculates that experimentalists have already encountered this kind of chaos. Projects that went awry the second time around could have been a result of the mischievous property of riddled basins. "I have a sneaking suspicion this might be the case for some," he intones. -Philip Yam