Brian Hayes
Digital computers are built out of circuits that have definite, discrete states: on or off, zero or one, high voltage or low voltage. Engineers go to great lengths to make sure these circuits never settle into some intermediate condition. Quantum-mechanical systems, as it happens, offer a guarantee of discreteness without any engineering effort at all. When you measure the spin orientation of an electron, for example, it is always either "up" or "down," never in between. Likewise an atom gains or loses energy by making a "quantum jump" between specific energy states, without passing through intermediate energy levels. So why not build a digital computer out of quantum-mechanical devices, letting particle spins or the energy levels of atoms stand for binary units of information?
One answer to this "Why not?" question is that you can't avoid building a quantum-mechanical computer even if you try. Since quantum mechanics appears to be a true theory of nature, it governs all physical systems, including the transistors and other components of the computer on your desk. All the same, quantum effects are seldom evident in electronic devices; components and circuits are designed so that the quantum states of many millions of electrons are averaged together, blurring their discreteness.
In a quantum computer, the basic working parts would probably have to be individual electrons or atoms, and so another answer to the "Why not?" question is that building such a machine is simply beyond our skills. And even apart from the challenges of atomic-scale fabrication, there are some ticklish conceptual issues. Quantum systems have some famously weird behavior, such as the phenomenon called quantum interference. Two nearby transistors can switch on and off independently, but two adjacent quantum objects (such as two electrons) are inextricably coupled, so that the future state of one electron cannot be predicted without taking into account the surrounding electrons. Indeed, an isolated electron can interfere with itself!
A third answer to the "Why not?" question is "Why bother?" Until recently there was no reason to believe that a quantum computer could do anything a classical computer couldn't. This situation has now changed dramatically. The exact place of quantum technology in the overall hierarchy of computing machines is still not settled, but a few recently discovered algorithms offer intriguing hints. It turns out that a program written for a quantum computer can factor large numbers faster than any known algorithm for a classical machine. The quantum factoring algorithm makes essential use of interference effects, which become a source of parallelism, allowing the computer to explore all possible solutions to a problem simultaneously. Factoring is a task of much theoretical interest, and it also has practical applications in cryptography, so these discoveries have attracted considerable notice.
Feynman's Question
An early investigator of quantum computing was the physicist Richard P. Feynman (1), although he looked at the issue mainly through the other end of the telescope, asking not what quantum mechanics could do for computing but what computing could contribute to the understanding of quantum physics. A classical computer bogs down when it is made to simulate a quantum system; Feynman suggested that a quantum computer might be better suited to the task.
At about the same time, Paul Benioff of the Argonne National Laboratory devised an elaborate quantum-mechanical simulation of a Turing machine, the standard benchmark of classical computing (2). Then in 1985 David Deutsch of the University of Oxford published another conceptual model of a quantum computer, one relying directly on the interference of quantum states (3). In 1992 Deutsch and Richard Jozsa, also of Oxford, formulated a few problems that could be solved faster with such a quantum computer than with a conventional Turing machine (4). This was the first direct evidence that quantum computers might be superior to classical ones.
There followed a sequence of papers reporting further developments and refinements in quantum computing (5, 6, 7), but the most arresting news was the announcement of a quantum-mechanical algorithm for factoring, devised by Peter W. Shor of AT&T Bell Laboratories (8). In all known classical factoring algorithms, the amount of time needed to find the prime factors of a number grows as an exponential function of the size of the number, making the algorithms impractical for very large numbers. (The factoring record at the moment is less than 150 decimal digits.) With Shor's quantum algorithm, the time needed grows as a polynomial function of the number's size. For example, factoring an n-digit number by classical methods might require 2n steps (an exponential function) whereas the quantum algorithm could find the factors in n2 steps (a polynomial). (The actual functions are different from these, but for any choice of functions, there is always a value of n beyond which the exponential function is larger than the polynomial one.)
Logic Gates
Conventional computers are built out of Boolean logic gates, notably those that implement the logic functions AND, OR and NOT. What are the corresponding primitive elements of a quantum computer? These building blocks too can be conceived as logic gates, but they operate on a very different kind of logic, in which probabilities play a crucial role. What follows is a sketch of the ideas underlying the construction of quantum logic gates. It is based on a lucid expository article by Gilles Brassard of the Université de Montreal (9) and on a talk that Shor delivered in March at the University of Maryland Baltimore County.
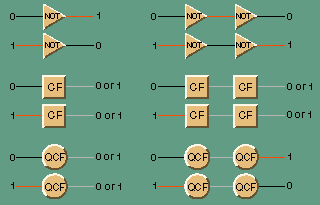
The simplest classical Boolean device is the NOT gate, which accepts a single bit of input and produces a single bit of output; the action of the gate is to negate or invert the input. In other words, if the input is a 0, the output is a 1; if the input is a 1, the output is a 0. Two NOT gates connected in series restore the input to its original state: An initial 0 is changed to a 1 by the first gate and then changed back to a 0 by the second gate. Thus a double negative is equivalent to the identity function.
The NOT gate is wholly deterministic: Once the input is known, the output is determined with absolute certainty. Suppose we relax this standard of determinism somewhat, creating a probabilistic logic gate that usually inverts its input--say 90 percent of the time--but occasionally passes the input through unchanged. This transformation can be represented by a probability matrix, as follows:
Here the numbers along the left edge, labeling the rows of the matrix, are the inputs to the gate, and the column labels at the top are the outputs. To find the probability that an input of 0 produces an output of 1, you read along the 0 row to where it intersects the 1 column. Note that even though the entries in the matrix are fractional values, this "probably NOT" gate is still a binary device whose inputs and outputs are always either 0 or 1. Also note that the probabilities in each column and each row sum to 1, indicating that every possible combination of input and output has been accounted for.
The operation of the simple deterministic NOT gate can be represented in the same matrix notation. Here is the transformation matrix:
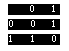
In this case the probability of getting a 0 output from a 0 input is 0 (it will never happen) whereas the probability of transforming a 0 into a 1 is 1 (certainty).
At the opposite pole from a completely deterministic logic gate is one that completely randomizes its input, producing a 0 or 1 output with equal probability. The transformation matrix for this function is:
![]()
In effect, the gate models a fair coin flip, and so it is designated CF. (A gate of this kind may seem totally useless, but in fact randomness is an important resource in certain algorithms.)
Quantum Logic Gates
Both the ordinary Boolean NOT gate and the probabilistic versions of it are still constructions of classical physics. A quantum-mechanical gate is far stranger. The strangeness goes to the very root of the quantum-computational process, to the bits themselves, which to emphasize their unconventional nature are sometimes called qubits. Whereas classical bits have the value 0 or 1 at all moments, qubits can occupy a "superposition" of the 0 and 1 states during certain stages of a computation. This is not to say that the qubit has some intermediate value between 0 and 1. Rather, the qubit is in both the 0 state and the 1 state at the same time, to varying extents. When the state of the qubit is eventually observed or measured, it is invariably either 0 or 1.
Quantum states and their superpositions are represented by means of a notational device called a ket, written "| >." The state of a qubit is given as a|0>+b|1>, where the coefficients a and b are the "amplitudes" of each state. In general the amplitudes are complex numbers (with both a real and an imaginary part), but the examples considered here will be confined to positive and negative real numbers. The amplitude associated with a state determines the probability that the qubit will be found in that state; specifically, the probability is equal to the square of the absolute value of the corresponding amplitude.
The relation between amplitude and probability can be made clearer with an example. A quantum gate that Brassard designates QCF (for "quantum coin flip") has the following matrix of amplitudes:
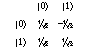
To find the probability of each of these transitions, take the absolute value of the corresponding amplitude and square it: |1/square root of 2|2 is equal to 1/2, and so is |-1/square root of 2|2. Thus all the entries in the probability matrix are 1/2, and the quantum-mechanical QCF gate appears on first examination to be identical to the classical CF gate. Either a 0 or a 1 signal passing through the QCF gate has an equal chance of coming out a 0 or a 1.
Under the surface, however, the CF and QCF gates are not at all alike. A way to see the difference is to link two gates in series. As noted above, two NOT gates in sequence compose the identity function. Two CF gates are also easy to analyze. Whatever the value of the initial input, the first CF gate produces a 0 or a 1 at random, and the second gate randomizes this value again. Hence any number of CF gates in sequence are equivalent in function to a single CF gate.
Two QCF gates in series work very differently. In a quantum-mechanical system it is not possible to assign a definite value to the unobserved intermediate signal between the two gates. The output of the first QCF gate is not a 0 or a 1 but a superposition of |0> and |1> states. Specifically, if the input to the first gate is a 1, the output of that gate is the superposition 1/square root of 2|0> +1/square root of 2|1>, as indicated by the matrix of amplitudes. Now this superposition of states becomes the input to the second QCF gate, which acts on it according to the same amplitude matrix. The 0 part of the superposition gets transformed into 1/square root of 2(1/square root of 2|0>-1/square root of 2|1>), while the 1 part becomes 1/square root of 2(1/square root of 2|0>+1/square root of 2|1>). Thus the entire state of the system becomes
![]()
Multiplying out the various factors of 1/square root of 2 yields 1/2(|0>-|1> + |0>+ |1>); now the +|1> and -|1> components cancel, leaving 1/2(|0>+ |0>), or simply |0>. A similar analysis shows that when the input to the first gate is a 0, the output observed at the second gate is a 1. The two gates implement the NOT function: (QCF)2 = NOT. Accordingly, a single QCF gate is said to calculate "the square root of NOT."
There is something decidedly counterintuitive about these results. Passing a signal through one QCF gate randomizes it, yet putting two QCF gates in a row yields a deterministic result. It is as if we had invented a machine that first scrambles eggs and then unscrambles them. There is no analogue of this machine in the more familiar world of classical physics.
The source of these odd effects is the phenomenon of quantum interference. The superposition of states can be thought of as a superposition of waves, which either reinforce or cancel depending on their amplitude and phase. Just as two coherent light sources combine to produce a pattern of light and dark "fringes," two quantum states interfere either constructively or destructively according to the sign of their amplitudes.
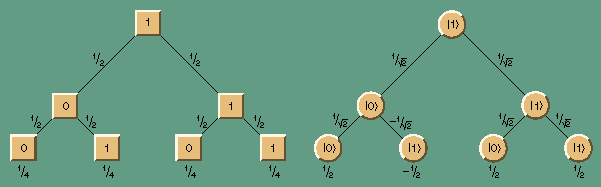
Consider again what happens when two CF gates or two QCF gates are wired in series. In the classical case, there are four possible sequences of events, which can be imagined as paths through the branches of a tree. Suppose the initial state, at the root of the tree, is a 1, and the first CF gate happens to produce a 0; the probability of this event is 1/2. Now if the second CF gate also emits a 0, again with probability 1/2, the overall probability of the entire 1-->0-->0 path is 1/2 x1/2, or 1/4. The other three paths, 1-->0-->1, 1-->1-->0 and 1-->1-->1, have the same probability of 1/4. Since two paths yield a 0 as the final state and two paths end in a 1, each of these outcomes has probability 1/2.
For QCF gates the analysis is framed in terms of amplitudes instead of probabilities. The first QCF gate transforms the initial |1> state into a |0> state with an amplitude of 1/square root of 2, then the second QCF gate produces a final |0> state with a further amplitude of 1/square root of 2. Multiplying these component amplitudes (just as one would multiply probabilities) yields an overall amplitude of 1/2 for the computational path |1> --> |0> --> |0>. The amplitude is the same for the paths |1> --> |1> --> |0> and |1> --> |1> --> |1>. In the case of the path |1> --> |0> --> |1>, however, the result is different; because the transition from |0> to |1> has an amplitude of -1/square root of 2, the total amplitude for this path is -1/2. In the absence of interference, this change of sign would still have no effect on the outcome of an experiment: Squaring the absolute value of each amplitude would yield four path probabilities of 1/4, which would sum to a probability of 1/2 for the |0> final state and 1/2 for the |1> final state. Because of interference, however, the two paths leading to the |1> state, with amplitudes of 1/2 and -1/2, cancel each other out, whereas the |0> paths, both with amplitudes of 1/2, sum to yield a total amplitude (and also a total probability) of 1.
Reversible Logic
The QCF gate demonstrates some principles of quantum computation, but it is not enough to build a complete quantum computer, any more than NOT gates are enough to build a classical computer. Performing useful calculations requires gates that process more than one bit (or qubit) at a time. For example, conventional computers make extensive use of and gates that accept two input bits and have a single output bit; the output is a 1 only if both input bits are 1's.
In designing gates for a quantum computer, certain constraints must be satisfied. In particular, the matrix of transition amplitudes must be unitary, which implies, roughly speaking, that it conserves probability: The sum of the probabilities of all possible outcomes must be exactly 1. A consequence of this requirement is that any quantum computing operation must be reversible: You must be able to take the results of an operation and put them back through the machine in the opposite direction to recover the original inputs. and gates do not obey this rule, since information is irretrievably lost when two input bits are condensed into a single output bit. Reversible gates must have the same number of inputs and outputs.
As it happens, the study of reversible computing has gotten a lot of attention lately, largely because of the discovery by Charles H. Bennett and Rolf Landauer of IBM that a reversible computer can perform any computation and can do so with arbitrarily low energy consumption (10). A reversible gate devised by Tommaso Toffoli of MIT is a "universal" classical gate: A computer could be built out of copies of this gate alone (11). Deutsch has shown that a similar gate is universal for quantum computers (12). Both the Toffoli and the Deutsch gates have three inputs and three outputs, but more recently two-qubit gates have also proved universal for quantum computations (13).
Practical quantum technologies are surely years or decades away, and yet a few implementation schemes are already under discussion. The idea closest to existing electronic technology relies on "quantum dots," which are isolated conductive regions within a semiconductor substrate (14). Each quantum dot can hold a single electron, whose presence or absence represents one qubit of information. Another proposal is based on a hypothetical polymeric molecule in which the individual subunits could be toggled between the ground state and an excited state (15). And David P. DiVincenzo of IBM has described a mechanism by which isolated nuclear spins would interact--and thereby compute--when they are brought together by the meshing of microscopic gears (13).
Quantum Parallelism
The extraordinary power of quantum computing comes from exploiting superposition and interference. Consider what happens when a classical computer is asked to search among all possible patterns of n bits for a particular pattern that satisfies some stated condition. With a single processor, the computer must examine each pattern sequentially, and since there are 2n such patterns, the task is intractable for large values of n. With parallel processing the search can be completed in a single step, but only if you can build 2n processors, which again becomes impractical as n grows large. A quantum computer might break the logjam, at least for some problems. After setting up the right initial superposition of states, and allowing it to evolve according to the right unitary transition matrix, a single quantum processor could sift through all the qubit patterns simultaneously. Destructive interference would suppress those patterns that were not of interest, while constructive interference would enhance those that met the stated conditions.
Factoring an integer can be formulated as such a search problem. The aim is to find a pattern of n/2 or fewer bits that evenly divides a given n-bit number. The simplest classical algorithm (albeit not the best one) searches for a factor by trial division, requiring either 2n/2 steps on a single processor or 2n/2 processors. In principle, a quantum computer might be designed to perform the search directly in a single step, by starting with a superposition of all 2n/2 qubit patterns and allowing them to interfere with one another according to some carefully crafted unitary transition matrix. When the computer halted, it would be in a state representing a factor of the number. Unfortunately, no one has any idea how to create the appropriate transition matrix or how to build a machine that would implement it.
Shor's quantum factoring algorithm is less direct, but it still relies on quantum interference to identify one special qubit pattern out of many. Quantum computation is used to solve the congruence xr = 1 modulo N, where N is the number to be factored and x is a random integer. Having found the least value of r that satisfies this relation, a straightforward classical calculation yields a factor of N.
If a quantum factoring algorithm is faster than any known classical algorithm, does that mean quantum computers are more powerful than classical ones? Curiously, the answer to this question is still unclear. Part of the difficulty of resolving it is that the computational status of factoring itself is uncertain. No classical polynomial-time factoring algorithm is known, but no one has proved that such an algorithm cannot exist. Thus factoring could yet turn out to be an "easy" problem, in which case the quantum computer's prowess in this special realm will not have much general significance. Far more convincing would be an efficient quantum method for a problem with better credentials attesting to its intractability, such as the traveling-salesman problem; but such a discovery is considered unlikely (16).
Whatever the theoretical standing of the factoring problem, its practical importance is unquestioned. "Public-key" cryptography depends for its security on the difficulty of factoring large integers. If it appears possible to build quantum computers, or even special-purpose quantum factoring engines, the secrecy of encrypted messages will be in jeopardy. But if quantum mechanics undermines one form of cryptography, it could also supply a replacement. Standing alongside the new study of quantum computing is the equally novel field of quantum cryptography, which derives its strength from the same mysterious physical laws.
References
1. Richard P. Feynman. 1982. Simulating physics with computers. International Journal of Theoretical Physics 21:467-488.
2. Paul Benioff. 1980. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. Journal of Statistical Physics 22:563-591.
3. David Deutsch. 1985. Quantum theory, the Church-Turing principle and the universal quantum computer. Proceedings of the Royal Society of London A400:97-117.
4. David Deutsch and Richard Jozsa. 1992. Rapid solution of problems by quantum computation. Proceedings of the Royal Society of London A439:553-558.
5. Andr Berthiaume and Gilles Brassard. 1994. Oracle quantum computing. Journal of Modern Optics 41:2521-2535.
6. Ethan Bernstein and Umesh Vazirani. 1993. Quantum complexity theory. Proceedings of the 25th Annual ACM Symposium on Theory of Computing, pp. 11-20.
7. Daniel R. Simon. 1994. On the power of quantum computation. Proceedings of the 35th Annual Symposium on Foundations of Computer Science, pp. 116-123.
8. Peter W. Shor. 1994. Algorithms for quantum computation: discrete logarithms and factoring. Proceedings of the 35th Annual Symposium on Foundations of Computer Science, pp. 124-134.
9. Gilles Brassard. 1994. Cryptology column--Quantum computing: The end of classical cryptography? SIGACT News 25(4):15-21.
10. Charles H. Bennett and Rolf Landauer. 1985. The fundamental physical limits of computation. Scientific American 253(1):48-56.
11. Tommaso Toffoli. 1980. Reversible computing. In Seventh Colloqium on Automata, Languages and Programming, J. W. de Bakker and J. van Leeuwen, eds. Berlin: Springer-Verlag. pp. 632-644.
12. David Deutsch. 1989. Quantum computational networks. Proceedings of the Royal Society of London A425:73-90.
13. David P. DiVincenzo. 1995. Two-bit gates are universal for quantum computation. Physical Review A 50:1015.
14. Craig S. Lent, Douglas Tougaw and Wolfgang Porod. 1994. Quantum cellular automata: The physics of computing with arrays of quantum dot molecules. Proceedings of the Workshop on Physics and Computation--Physcomp `94, pp. 5-13.
15. Seth Lloyd. 1993. A potentially realizable quantum computer. Science 261:1569-1571.
16. Charles H. Bennett, Ethan Bernstein, Gilles Brassard and Umesh V. Vazirani. 1994. Strengths and weaknesses of quantum computing. Preprint.
© Brian Hayes