Overview of Shor's Algorithm

Shor's algorithm hinges on a result from number theory. This result is: The function $\mathcal{F}(a) = x^{a} \bmod n$ is a periodic function, where x is an integer coprime to n. In the context of Shor's algorithm n will be the number we wish to factor. When two numbers are coprime it means that their greatest common divisor is 1.

Calculating this function for an exponential number of a's would take exponential time on a classical computer. Shor's algorithm utilizes quantum parallelism to perform the exponential number of operations in one step.

The reason why this function is of utility in factoring large numbers is this:

Since $\mathcal{F}(a)$ is a periodic function, it has some period r. We know that $x^{0} \bmod n = 1$ , so $x^{r} \bmod n = 1$ , and $x^{2r} \bmod n = 1$ and so on since the function is periodic.

Given this information and through the following algebraic manipulation:

$\begin{displaymath}x^{r} = 1 \bmod n\end{displaymath}$

$\begin{displaymath}(x^{r/2})^{2} = x^{r} = 1 \bmod n\end{displaymath}$

$\begin{displaymath}(x^{r/2})^{2} - 1 = 0 \bmod n\end{displaymath}$

and if r is an even number

$\begin{displaymath}(x^{r/2} - 1)(x^{r/2} + 1) = 0 \bmod n\end{displaymath}$

We can see that the product (x^r/2 - 1)(x^r/2 + 1) is an integer multiple of n, the number to be factored. So long as x^r/2 != +- 1, then at least one of (x^r/2 - 1), (x^r/2 + 1) must have a nontrivial factor in common with n. So by computing $\gcd(x^{r/2} - 1, n)$ , and $\gcd(x^{r/2} + 1, n)$ , we will obtain a factor of n, where $\gcd$ is the greatest common divisor function.

Here is a brief overview of Shor's algorithm, which is explained in detail in the next section. Shor's algorithm tries to find r, the period of $x^{a} \bmod n$ , where n is the number to be factored by Shor's algorithm, and x is an integer coprime to n. To do this Shor's algorithm creates a quantum memory register with two parts. In the first part the algorithm places a superposition of the integers which are to be a's in the $x^{a} \bmod n$ function. We will choose our a's to be the integers 0 through q - 1, where q is the power of two such that $n^{2} \leq q < 2n^{2}$ . Then the algorithm calculates $x^{a} \bmod n$ , where a is the superposition of the states, and places the result in the second part of the quantum memory register.

Next the algorithm measures the state of the second register, the one that contains the superposition of all possible outcomes for $x^{a} \bmod n$ . Measuring this register has the effect of collapsing the state into some observed value, say k. It also has the side effect of projecting the first part of the quantum register into a state consistent with the value measured in the second part. Since we have partitioned our quantum register into two parts measurement of the second part collapses that part into exactly one value, while the other partition collapses into a state consistent with the observed value in the other portion of the register. It is still possible for the non measured part of the register to exist in a superposition of base states, as long as each of those base states are consistent with the measured value in the other part of the register. What this means in this instance is that after this measurement the second part of the register contains the value k, and the first part of the register contains a superposition of the base states which when plugged into $x^{a} \bmod n$ produce k. Since we know $x^{a} \bmod n$ is a periodic function, we know that the first part of the register will contain the values c, c+r, $c+2r\ldots$ and so on, where c is the lowest integer such that $x^{c} \bmod n = k$ .

The next step is to perform a discrete Fourier transform on the contents of first part of the register (the one containing all integers such that $x^{a} \bmod n = k$ ) and to put the result back into register one. This Fourier transform maps functions in the time domain to functions in the frequency domain. The application of the discrete Fourier transformation has the effect of peaking the probability amplitudes of the first part of the register at integer multiples of the quantity q / r.

Now measuring the first part of the quantum register will yield an integer multiple of the inverse period. Once this number is retrieved from the quantum memory register, a classical computer can do some analysis of this number, make a guess as to the actual value of r, and from that compute the possible factors of n. This post processing will be covered in more detail later. (Shor)

Steps to Shor's Algorithm

Shor's algorithm for factoring a given integer n can be broken into some simple steps.

Step 1) Determine if the number n is a prime, a even number, or an integer power of a prime number. If it is we will not use Shor's algorithm. There are efficient classical methods for determining if a integer n belongs to one of the above groups, and providing factors for it if it is. This step would be performed on a classical computer.

Step 2) Pick a integer q that is the power of 2 such that $n^{2} \leq q < 2n^{2}$ . This step would be done on a classical computer.

Step 3) Pick a random integer x that is coprime to n. When two numbers are coprime it means that their greatest common divisor is 1. There are efficient classical methods for picking such an x. This step would be done on a classical computer.

Step 4) Create a quantum register and partition it into two sets, register 1 and register 2. Thus the state of our quantum computer can be given by: |reg1, reg2>. Register 1 must have enough qubits to represent integers as large as q - 1. Register 2 must have enough qubits to represent integers as large as n - 1. The calculations for how many qubits are needed would be done on a classical computer.

Step 5) Load register 1 with an equally weighted superposition of all integers from 0 to q - 1. Load register 2 with all zeros. This operation would be performed by our quantum computer. The total state of the quantum memory register at this point is:

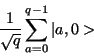
$\begin{displaymath}\frac{1}{\sqrt{q}}\sum_{a = 0}^{q - 1} \vert a, 0>\end{displaymath}$

Step 6) Now apply the transformation $x^{a} \bmod n$ to for each number stored in register 1 and store the result in register 2. Due to quantum parallelism this will take only one step, as the quantum computer will only calculate $x^{\vert a>} \bmod n$ , where |a> is the superposition of states created in step 5. This step is performed on the quantum computer. The state of the quantum memory register at this point is:

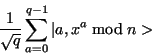
$\begin{displaymath}\frac{1}{\sqrt{q}}\sum_{a=0}^{q-1}\vert a,x^{a} \bmod n>\end{displaymath}$

Step 7) Measure the second register, and observe some value k. This has the side effect of collapsing register one into a equal superposition of each value a between 0 and q-1 such that

$\begin{displaymath}x^{a} \bmod n = k\end{displaymath}$

This operation is performed by the quantum computer. The state of the quantum memory register after this step is:

$\begin{displaymath}\frac{1}{\sqrt{\vert\vert A\vert\vert}}\sum_{a'=a'\in A}\vert a', k>\end{displaymath}$

Where A is the set of a's such that $x^{a} \bmod n = k$ , and ||A|| is the number of elements in that set.

Step 8) Now compute the discrete Fourier transform on register one. The discrete Fourier transform when applied to a state |a>changes it in the following manner:

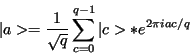
$\begin{displaymath}\vert a> = \frac{1}{\sqrt{q}}\sum_{c=0}^{q-1}\vert c>*e^{2\pi iac/q}\end{displaymath}$

This step is performed by the quantum computer in one step through quantum parallelism. After the discrete Fourier transform our register is in the state:

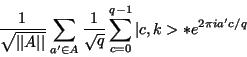
$\begin{displaymath}\frac{1}{\sqrt{\vert\vert A\vert\vert}}\sum_{a'\in A}\frac{1}{\sqrt{q}}\sum_{c=0}^{q-1} \vert c,k>*e^{2\pi ia'c/q}\end{displaymath}$

Step 9) Measure the state of register one, call this value m, this integer m has a very high probability of being a multiple of q/r, where r is the desired period. This step is performed by the quantum computer.

Step 10) Take the value m, and on a classical computer do some post processing which calculates r based on knowledge of m and q. There are many ways to do this post processing. This post processing is done on a classical computer.

Step 11) Once you have attained r, a factor of n can be determined by taking $\gcd(x^{r/2} + 1, n)$ and $\gcd(x^{r/2} - 1, n)$ . If you have found a factor of n, then stop, if not go to step 4. This final step is done on a classical computer.

Step 11 contains a provision for what to do if Shor's algorithm failed to produce factors of n. There are a few reasons why Shor's algorithm can fail, for example the discrete Fourier transform could be measured to be 0 in step 9, making the post processing in step 10 impossible. The algorithm will sometimes find factors of 1 and n, which is not useful either. For these reasons step 11 must be able to jump back to step four to start over. (Williams, Clearwater)