 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes live video seminars, enchanting renewal songs and a thousand page illustrated codex.
 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes
live video seminars, enchanting renewal songs and a thousand page
illustrated codex.
 Return
to Genesis of Eden?
Return
to Genesis of Eden?
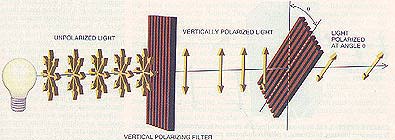
Unpolarised light enters a filter, which absorbs some of the
light and polarizes the ramainder in the vertical direction. A second filter
tilted at some angle absorbs some of the polarized light and transmits the
rest, giving it a new polarization.
Quantum Cryptography Scientific American Jul 92
CHARLES H. BENNETT, GILLES BRAS SARD and ARTUR K. EKERT
In his classic short story "The Gold Bug," published in 1843, Edgar Allan Poe explains the rudiments of code breaking and ventures the opinion that the human mind can break any cipher that human ingenuity could devise. During the subsequent century and a half, the contest between code makers and code breakers has undergone reversals and complications that would have delighted Poe. An unbreakable cipher was invented in 1918, although its unbreakability was not proved until the 1940s. TWs cipher was rather impractical because it required the sender and receiver to agree beforehand on a key-a large stockpile of secret random digits, some of which were used up each time a secret message was transmitted. More practical ciphers with short, reusable keys, or no secret key at all, were developed in the 1970s, but to this day they remain in a mathematical limbo, having neither been broken nor proved secure. A recent unexpected development is the use of quantum mechanics to perform cryptographic feats unachievable by mathematics alone. Quantum cryptographic devices typically employ individual photons of light and take advantage of Heisenberg's uncertainty principle, according to which measuring a quantum system in general disturbs it and yields incomplete information about its state before the measurement. Eavesdropping on a quantum communications channel therefore causes an unavoidable disturbance, alerting the legitimate users. Quantum cryptography exploits this effect to allow two parties who have never met and who share no secret information beforehand to commuriicate in absolute secrecy under the nose of an adversary. Quantum techriiques also assist in the achievement of subtler cryptographic goals, important in the post-cold war world, such as enabling two mutually distrustful parties to make joint decisions based on private information, while compromising its confidentiality as little as possible.
The art of cryptography began at least 2,500 years ago and has played an important role in history ever since. Perhaps one of the most famous cryptograms, the Zimmermann Note, propelled the U.S. into World War 1. When the cryptogram was broken in 1917, Americans teamed that Germany had tried to entice Mexico to join its war effort by promising Mexico territories in the U.S. Around this time Gilbert S. Vernam of American Telephone and Telegraph Company and Major Joseph O' Mauborane of the U.S. Army Signal Corps developed the first truly unbreakable code called the Vernam cipher [see below]. One distinctive feature of the code is its need for a key that is as long as the message being transniitted and is never reused to send another message. (The Vernam cipher is also known as the one-time pad from the practice of furnishing the key to spies in the form of a tear-off pad, each sheet of which was to be used once and then carefully destroyed.) The discovery of the Vernam cipher did not create much of a stir at the time, probably because the cipher's unbreakabflity was not definitively proved until later and because its massive key requirements made it impractical for general use.
Because of this limitation soldiers and diplomats continued to rely on weaker ciphers using shorter keys. Consequently, during World War II, the Allies were able to read most of the secret messages transmitted by the Germans and Japanese. These ciphers, though breakable, were by no means easy to crack. Indeed, the formidable task of breaking increasingly sophisticated ciphers was one of the factors that stimulated the development of electronic computers. Academic interest in cryptology grew more intense in the mid-1970s, when Whitfield Diffie, Martin E. Heflman and Ralph C. Merkle, then at Stanford University, discovered the principle of public-key cryptography (PKC). Soon afterward, in 1977, Ronald L. Rivest, Adi Shamir and Leonard M. Adleman, then at the Massachusetts Institute of Technology, devised a practical implementation. Public-key cryptosystems differ from all previous schemes in that parties wishing to communicate do not need to agree on a secret key beforehand. The idea of PKC is for a user, whom we shall call Alice, to choose randomly a pair of mutually inverse transformations-to be used for encryption and decryption; she then publishes the instructions for performing encryption but not decryption. Another user, Bob, can then use Ahce's public-encryption algorithm to prepare a message that only she can decrypt. S@arly, anyone, including Alice, can use Bob's public encryption algorithm to prepare a message that only he can decrypt. Thus, Alice and Bob can converse secretly even though they share no secret to begin witIL Public-key cryptosystems are especially suitable for encrypting electronic mail and commercial transactions, wmch often occur between parties who, unlike diplomats and spies, have not anticipated their need to communicate secretly. Offsetting this advantage is the fact that public-key systems have not been proven to be secure. Indeed, in 1982 Shamir, now at the Weizmann Institute of Science in Israel, cracked one of the early public-key cryptosystems, the knapsack cipher. Poe could be smiling from the grave, knowing there is a clever method of attack, as yet undiscovered, that could break any of these ciphers in a few minutes.
Several years before the discovery of public-key cryptography, an other striking development had quietly taken place: the union of cryptography with quantum mechanics. Around 1970 Stephen J. Wiesner, then at Columbia University, wrote a paper entitled "Conjugate Coding," explaining how quantum physics could be used, at least in principle, to accomplish two tasks that were impossible from the perspective of classical physics. One task was a way to produce bank notes that would be physically impossible to counterfeit. The other was a scheme for combining two classical messages into a single quantum transmission from which the receiver could extract either message but not both. Unfortunately, Wiesner's paper was rejected by the journal to which he sent it, and it went unpublished until 1983. Meanwhile, in 1979, two of us (Bennett and Brassard) who knew of Wiesner's ideas began thinking of how to combine them with public-key cryptography. We soon realized that they could be used as a substitute for PKC: two users, who shared no secret initially, could communicate secretly, but now with absolute and provable security, barring violations of accepted physical laws. Our early quantum cryptographic schemes, developed between 1982'and 1984, were somewhat impractical, but reftnements over the next few years culminated in the building of a fully working prototype at the MM Thomas J. Watson Research Center in 1989. John Smolin, now at the University of California at Los Angeles, helped to build the electronics and optics for the apparatus, and Fran@ois Bessette and Louis Salvail of the University of Montreal assisted in writing the software. At about the same time, the theoretical ideas of David Deutsch of the University of Oxford led one of us (Ekert) to conceive of a slightly different cryptosystem based on quantum correlations. In early 1991, utilizing ideas conceived by Massiino Palma of the University of Palermo, John Rarity and Paul Tapster of the British Defence Research Agency started experiments implementing Ekert's cryptosystem. To explain how such systems work, we need to describe in more detail some aspects of the mathematics of classical cryptography, especially the role of the key. In the early days of cryptography the security of a cipher depended on the secrecy of the entire encryption and decryption procedure. Today such procedures are usually known publicly, but the key is kept secret. In such ciphers the key is used to control and customize the encryption and decryption processes in such a way that an adversary who has intercepted the cryptogram and knows the general method of encryption but not the key wfll not be able to infer anything useful about the original message. Consequently, the cryptogram may be broadcast over a public channel such as a radio or printed in a newspaper. The key, however, must be sent through a very secure private channel, such as a clandestine meeting or a delivery by a trusted courier. Although the distribution of a key over private channels is expensive, it makes possible subsequent secret communication over inexpensive public channels. Ultimately, the security of a cryptogram depends on the length of the key. In two brilliant papers written in the 1940s, Claude E. Shannon, then at Beu Laboratories, showed that if the key is shorter ffim the message being encrypted, some information about the message can be inferred from the cryptogram by a sufficiently powerful adversary. This leakage of information occurs regardless of how complicated the encryption process may be. In contrast, the message can be completely and unconditionally hidden from the eavesdropper by cryptosystems such as the Vernam cipher, in which the key is as long as the message, is purely random and is used only once.
Even the Vernam cipher is only as secure as its key distribution and key storage. Because of the great difficulty of supplying secure new keys for every message, the Vernam cipher is impractical for general commercial uses, although it is routinely employed for diplomatic communications such as those exchanged over the Moscow-Washington hot hne. hi contrast, the most widely used commercial cipher, the Data Encryption Standard, depends on a 56-bit secret key, which is reused for many encryptions over a certain length of time. This scheme simplifies the problem of secure key distribution and storage, but it does not eliminate it. A fundamental problem remains. In principle, any classical private channel can be monitored passively, without the sender or receiver knowing that the eavesdropping has taken place. For example, a key carried by a trusted courier might have been read en route by a surreptitious high-resolution x-ray scan or other sophisticated imaging technique without the courier's knowledge. More generally, classical physics-the theory of macroscopic bodies and phenomena such as paper documents, magnetic tapes and radio signals-allows aR physical properties of an object to be measured without disturbing those properties. Since all information, induding a cryptographic key, is encoded in measurable physical properties of some object or signal, classical theory leaves open the possibility of passive eavesdropping, because it allows the eavesdropper in principle to measure physical properties without disturbing them. This is not the case in quantum theory, which forms the basis for quantum cryptography. Quantum theory is believed to govern all objects, large and small, but its consequences are most conspicuous in microscopic systems such as individual atoms or subatomic particles. The act of measurement is an integral part of quantum mechanics, not just a passive, extemal process as in classical physics. So it is possible to design a quantum channel-one that carries signals based on quantum phenomena-in such a way that any effort to monitor the channel necessarily disturbs the signal in some detectable way. The effect arises because in quantum theory, certain pairs of physical properties are complementary in the sense that measuring one property necessarily disturbs the other. This statement, known as the Heisenberg uncertainty principle, does not refer merely to the limitations of a particular measurement technology: it holds for all possible measurements. The uncertainty principle can be applied to design a completely secure channel based on the quantum properties of light. The smallest unit, or quantam, of light is the photon, which can be thought of as a tiny, oscillating electric field. The direction of the oscfllation is known as the photon's polarization. Ordinary light consists of photons that have many different polarizations. But if the light passes through a polarizing ffiter, such as those used in sunglasses, only photons having a particular polarization will make it through. WWch polarization is transmitted depends on the orientation of the fflter. In sunglasses the fflters are oriented to transmit vertically polarized light because such light reflects off most horizontal surfaces with less glare. But if the glasses are turned 90 degrees, so that one lens is directly above the other, they will transmit horizontally polarized light, augmenting the glare instead of diminishing it.
To construct a quantum channel, one needs a polarizing filter or other means for the sender to prepare photons of selected polarizations and a way for the receiver to measure the polarization of the photons. The latter job could be accomplished by another polarizing filter, which would absorb some of the photons striking it. But the task is most conveniently done by a birefringent crystal (such as calcite), which sends incident photons, depending on their polarization, into one of two paths without absorbing any [see illustration]. A photon encountering a calcite crystal behaves in one of two ways depending on its polarization in relation to the crystal. The photon may pass straight through the crystal and emerge polarized perpendicular to the crystal's optic axis, or it may be shifted and emerge polarized along that axis. If the photon entering the crystal is already polarized in one of these two directions, it will undergo no change of polarization but will be deterministically routed into the straight or shifted path, respectively. If a photon polarized at some intermediate direction enters the crystal, however, it will have some probability of going into each beam and will be repolarized according to which beam it goes into, forgetting its original polarization. The most random behavior occurs when the photon is polarized halfway between these two directions, that is, at 45 or 135 degrees. Such photons are equally likely to go into either beam, revealing nothing about their original polarization and losing all memory of it. Suppose Bob is told in advance that a given photon is polarized in one of the two "rectilinear" directions, vertical (90 degrees) or horizontal (O degrees) without being informed of the specific polarization. Then he can reliably tell which direction by sending the photon into an apparatus consisting of a vertically oriented calcite crystal and two detectors, such as photomultiplier tubes, that can record single photons. The calcite crystal directs the incoming photon to the upper detector if it was horizontally polarized and to the lower detector if it was vertically polarized. Such an apparatus is useless for distinguishing diagonal (4 5or 13 5-degree) photons, but these can be reliably distinguished by a similar apparatus that has been rotated 45 degrees from the original orientation. The rotated apparatus, in tum, is useless for distinguishing vertical from horizontal photons. According to the uncertainty principle, these limitations apply not just to the particular measuring apparatus described here but to any measuring device whatsoever. Rectflinear and diagonal polarizations are complementary properties in the sense that measuring either property necessarily randorriizes the other. We can now describe the simple scheme for quantum key distribution that two of us (Bennett and Brassard) proposed in 1984 and that we dubbed "BB84." The purpose of the scheme is for Ahce and Bob to exchange a secret random key that they can subsequently use, as in the Vernam cipher, to send meaningful secret messages when the need arises. like other quantum key distribution schemes, BB84 uses a quantum channel, through which Alice and Bob send polarized photons, in conjunction with a classical pubhc channel, through which they send ordinary messages. An eavesdropper, whom we shall call Eve, is free to try to measure the photons in the quantum channel, but, as noted above, she cannot in general do this without disturbing them. Furthermore, she learns the entire contents of messages sent through the public channel but assume for the moment that she could not disturb or alter these messages even if she wanted to.
Alice and Bob use the public channel to discuss and compare the signals sent through the quantum channel, testing them for evidence of eavesdropping. If they find none, they can distill from their data a body of information that is certifiably shared, random and secret, regardless of Eve's technical sophistication and the computing power at her disposal [see box on opposite page]. The scheme works as follows: First, Alice generates and sends Bob a sequence of photons whose polarizations she has chosen at random to be either 0, 45, 90 or 135 degrees. Bob receives the photons and, for each photon, decides randomly whether to measure its rectilinear or diagonal polarization.
Next Bob announces publicly, for each photon, which type of measurement he has made (rectilinear or diagonal) but not the measurement result (for example, 0, 45, 90 or 135 degrees). Alice tells him publicly, for each photon, whether he has made the right kind of measurement. Ahce and Bob then discard au cases in which Bob has niade the wrong measurement or in which his detectors have failed to register a photon at au (e)dsting detectors are not 100 percent efficient). If no one has eavesdropped on the quantum channel, the remaining polarizations should be shared secret information between Alice and Bob. Ahce and Bob next test for eavesdropping, for example, by publicly comparing and discarding a randon-Ay selected subset of their polarization data. If the comparison test shows evidence of eavesdropping, Alice and Bob discard all their data and start over with a fresh batch of photons. Otherwise they adopt the remaining polarizations, which have never been publicly mentioned, as shared secret bits, interpreting horizontal or 45-degree photons as binary O's and vertical or 135-degree photons as binary I's. Because of the uncertainty principle, Eve cannot measure both rectilinear and diagonal polarizations of the same photon. If, for a particular photon, she makes the wrong measurement, then, even if she resends Bob a photon consistent with the result of her measurement, she wffl have irretrievably randorriized the polarization originally sent by Alice. The net effect is to cause errors in one quarter of the bits in Bob's data that have been subjected to eavesdropping.
Directly comparing selected bits to test for errors, as described above, is not very efficient: too many bits must be sacrificed in order to build reasonable confidence that Alice's and Bob's data are identical, especially if the eavesdropping has been rather infrequent, resulting in only a few errors. A much better idea is for Alice and Bob to compare the "parity"-evenness or oddness-of a publicly agreed-on random subset containing about half the bits in their data. For instance, Alice could tell Bob, "I looked at the lst, 3rd, 4th, 9th .... 996th and 999th of my 1,000 bits of data, and they include an even number of l's." Bob would then count the number of 1's that he has in those same locations. If he finds an odd number of l's, he can immediately conclude that his data are different from Alice's. it can be shown that if Alice's and Bob's data differ, comparing the parity of a random subset will detect that fact with a probability of 1/2, regardless of the number and location of errors. It suffices to repeat the test 20 times, with 20 different random subsets, to reduce the chance of an undetected error to less than one in a million.
The BB84 scheme was modified to produce a working quantum cryptography apparatus at IBM [see illustration on pages 32 and 331. The modifications were necessary to deal with practical problems such as noise in the detectors and the fact that the prototype uses dim flashes of light instead of single photons.
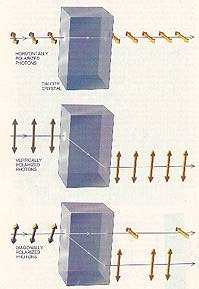 Calcite CRYSTAL can be used to distinguish between horizontally
and vertically polarized photons. Horizontally polarized photons pass straight
through, whereas vertically polarized photons are deflected. When diagonally
polarized photons enter the crystal, they are repolarized at random in either
the vertical or horizontal direction and are shifted accordingly.
Calcite CRYSTAL can be used to distinguish between horizontally
and vertically polarized photons. Horizontally polarized photons pass straight
through, whereas vertically polarized photons are deflected. When diagonally
polarized photons enter the crystal, they are repolarized at random in either
the vertical or horizontal direction and are shifted accordingly.
The quantum channel, with Alice's sending apparatus at one end and Bob's receiving apparatus at the other, is housed in a light-tight box. During operation, the system is controlled by a personal computer, which contains separate software representations of Ahce, Bob and, optionally, Eve. The leftmost part of Alice's sending apparatus consists of a green light-eniitting diode, a lens, a pinhole and Mters that provide a collimated beam of horizontaHy polarized light. Next, electrooptic devices known as Pockels cells are used to change the original horizontal polarization to any of four standard polarization states under Alice's control. This has the same effect as mechanically rotating her polarizing fflter into four different positions, but the process can be done much faster. At the other end of the quantum channel, Bob's receiving apparatus contains a siniflar Pockels cell, which allows him to choose the type of polarization he will measure, again without actually rotating his detecting device. After the beam passes through Bob's Pockels cell, it is split by a calcite prism into two perpendicularly polarized beams, which are directed into two photomultiplier tubes for the purpose of detecting individual photons. The sending and receiving apparatuses in the prototype are only about 30 centimeters apart-chiefly because of the desire to keep the device of reasonable dimensions for a desktop-but nothing in principle prevents the technique from being used over much greater distances. For example, quantum transmissions could be sent through several kilometers of optical fiber. If cost and inconvenience were no concem, quantum transmissions could be sent over arbitrarily great distances with negligible losses through an evacuated straight pipe. But quantum key distribution has to compete with classical techniques, which are much cheaper over long distances and may be sufficiently secure. Recall that the BB84 scheme encodes each bit in a single polarized photon. In contrast, the prototype encodes each bit in a dim flash of light. This introduces a new eavesdropping threat to the system: if Eve taps into the beam by a device such as a half-silvered n-Arror, she wffl be able to split each flash into two flashes of lesser intensity, reading one herself while letting the other pass to Bob, its polarization undisturbed. if Eve diverts only a modest fraction of the beam, Bob may not notice the weakening of his signal, or he may attribute it to natural losses in the channel. This attack can be effectively thwarted, at the cost of reducing the rate of data transmission through the quantum channel, by having Alice send very dim flashesthat is, an intensity of less than one photon per flash on average. Such extremely dim flashes can easily be made by ffltering out almost aH the intensity of a bright flash. When low-intensity flashes are used, Bob's chance of detecting a photon in any given flash is of course proportionately reduced, but the chance of Bob and Eve both detecting photons in the same flash is reduced even more, as the square of the intensity. The actual apparatus generates intensities of about one tenth of a photon per flash. On the other hand, if Alice's flashes were much brighter (say, thousands of photons per flash), they would be easy prey for the beam-splitting attack. By splitting off only a small fraction of the intensity, Eve could stffl obtain enough photons from each flash to perform both rectilinear and diagonal measurements and so determine the polarization unambiguously. In other words, the brighter Alice's flashes, the more they behave like classical signals, about which an eavesdropper can gain complete information while introducing negligible disturbance. Another practical problem arises from the fact that available detectors sometimes produce a response even when no photon has arrived. Such "dark counts" and other imperfections in the apparatus lead to errors even when there has been no eavesdropping and make it impractical for Alice and Bob simply to reject their data whenever they find an error in them, as is done in the ideal BB84 protocol.
Quantum Key Distribution
Quantum cryptographic system will allow two people, say, Alice and Bob, to exchange a secret key. The system includes a transmitter Aand a receiver. Alice uses the transmitter to send photons in one of four polarizations: 0, 45, 90 or 135 degrees. Bobs uses the receiver to measure the polarization. According to the laws of quantum mechanics, the receiver can distinguish between rectilinear polarizations (O and 90), or it can quickly be reconfigured to discriminate between diagonal polarizations (45 and 135); it can never, however, distinguish both types. The key distribution requires several steps. Alice sends photons with one of fo u r polarizations, which she has chosen at random.
![]()
For each photon, Bob chooses at random the type of measurement: either the rectilinear type (+) or the diagonal type (x).
![]()
Bob records the result of his measurement but keeps it a secret.
![]()
Bob publicly announces the type of measurements he made, and Alice tells him which measurements were of the correct type.
![]()
Alice and Bob keep all cases in which Bob measured the correct type. These cases are then translated into bits (I's and O's) and thereby become the key.
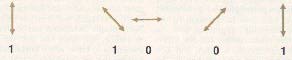
If Bob and Alice find a small number of errors, they must devise a way to correct them and proceed. On the other hand, if they find a large number, indicating significant eavesdropping, they must reject their data and start over.
A variety of techniques are available for Alice and Bob to correct a small number of errors through public discussion, such as the use of error-correcting codes. But these techniques potentially leak information to Eve, who may be listening to the public discussion. Therefore, after the quantum transmission and the errorcorrecting discussion, Alice and Bob find themselves with what might be thought of as an impure key, a shared body of data that is ortly partly secret. Information on that key may have leaked to Eve at several stages. She may have gained information by splitting some flashes, by directly measuring others (she cannot do this too often, as it causes errors in Bob's data) and by listening to the public discussion between Alice and Bob. Fortunately, Alice and Bob, because they know the intensity of the light flashes and the number of errors found and corrected, can estimate how much information might have leaked to Eve through all these routes. in itself, such an impure key is almost worthless. If it were used as a key for the Vernam cipher, for example, it might prove very insecure if the most important part of the message happened to coincide with a part of the key the eavesdropper knew. Fortunately, two of us (Bennett and Brassard), in couaboration with Jean-Marc Robert (then a student of Brassard), developed a mathematical technique known as privacy amplification. Using this technique, Alice and Bob, through public discussion, can take such a partly secret key and distill from it a smaller amount of highly secret key, of which the eavesdropper is very unlikely to know even one bit. The essential idea of privacy amplffication is for Alice and Bob, after the eavesdropping has taken place, to choose publicly a length-reducing transformation to apply to their impure key so that partial information about the input conveys almost no knowledge of the output. For example, if the input consists of 1,000 bits about which Eve knows at most 200 bits, Alice and Bob can distill nearly 800 highly secret bits as output. Fairly simple techniques can be shown to suffice, and Alice and Bob do not even need to know which partial information the eavesdropper might have about the input in order to choose a function about whose output Eve has almost no information. In particular, it suffices for Alice and Bob to define each bit of the output as the parity of an independent, publicly agreed-on random subset of the input bits, very much as they had done to gain high confidence that their raw quantum data were identical (except that now they keep the parity secret instead of pubhcly comparing it).
The problem of key security is not entirely solved by secure key distribution. Another weak point is key storage. Once Alice and Bob have established the key, they must store it until it is needed. But the longer they keep the key in, say, their secret safe, the more vulnerable it is to unauthorized inspection. Although principles of engineering may make the safe difficult to crack, the laws of physics always provide the possibility of a security breach. Surprisingly, a cryptosystem can be designed that can guarantee the security of both key diswbution and storage by employing quantum correlations. The cryptosystem is based on David Bohm's version of the famous Einstein-Podolsky-Rosen (EPR) effect. The EPR effect occurs when a spherically symmetric atom emits two photons in opposite directions toward two observers, Alice and Bob. The two photons are produced in an initial state of undefined polarization. But because of the symmetry of the initial state, the polarizations of the photons, when measured, must have opposite values, provided that the measurements are of the same type. For example, if Ahce and Bob both measure rectilinear polarizations, they are each equally likely to record either a 0 (horizontal polarization) or a 1 (vertical), but if Alice obtains a 0, Bob wffl certainly obtain a 1, and vice versa. The unusual and important aspect of the EPR effect is that the polarization of both photons is determined as soon as, but not before, one of the photons is measured. TWs happens no matter how far apart the photons may be at the time. This "classical" explanation of the EPR effect is somewhat counterintuitive, and indeed all classical explanations of the EPR effect involve some implausible element, such as instantaneous action at a distance. Yet the mathematical formalism of quantum mechanics accounts for the EPR effect in a straightforward manner, and experiments have amply confirmed the e)dstence of the phenomenon. Employing the EPR effect, one of us (Ekert) recently devised a cryptosystem that guarantees the security of both key distribution and key storage.
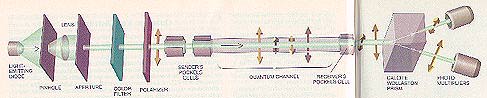
QUANTUM SYSTEM can distribute information in perfect secrecy.
The transmitter produces faint flashes of green light from a light-emitting
diode. The pinhole, lens and filter create a collimated beam of dim flashes.
The light is then pomzed horizontally. Two Pockels cells change the polarization
to 0, 45, 90 or 135 degrees. The polarised light flashes are released from
the transmitter and eventually reach the receiver.Ibere another Pockets
cell shifts the polarization by either 45 degrees or not at ala The action
of this Pockets cell allows the receiver to choose between measuring rectilinear
or diagonal polarization. In the rectilinear case, a horizontally polarized
photon will be directed toward the right photomultiplier; a vertically polarized
photon will be directed toward the left photomultiplier.
In a simplified version of this system, as described by N. David Mermin of Cornell University, Alice generates a number of EPR photon pairs, keeping one member of each pair for herself while sending the other to Bob. Alice and Bob measure some of their photons inimediately to test for eavesdropping but store the remainder without measuring them. Then, just before the key is needed, they measure and compare some of the stored photons. if no one has tampered with the photons in storage, Bob wm always obtain I when Ahce obtains 0, and vice versa. If no discrepancies are found, Ahce and Bob measure the remaining stored photons to obtain the desired key. Although this procedure works in theory, it cannot be used in practice because of the technical infeasibility of storing photons for more than a small fraction of a second. Thus, at present, the EPR effect is not a practical means for certifying the security of key storage.
Although the best-known application of cryptography is secret Acommunication, two other applications are probably more important in peacetime. The first is authentication: certifying that a message is from whom it says it is from and has not been altered in transit. The second is the task of maintaining the confidentiality of private information while it is being used to reach public decisions. For most of recorded history, authentication has depended on physical objects that are hard to copy, such as seals and signatures. Such devices provide limited security, and they cannot be used at all for digital electronic documents, such as bank transactions, which are often transmitted over insecure telecommunications lines.
Fortunately, several mathematical techniques are available for authenticating digital messages. In 1979 Mark N. Wegman and J. Lawrence Carter of IBM discovered a digital authentication scheme that does provide provable security. Like the Vernam cipher, it requires that the sender and receiver possess beforehand a shared secret key, part of which is used up each tune a message is authenticated. Wegman-Carter authentication and quantum key distribution can each benefit the other. On the one hand, the quantum technique supplies the secret key bits consumed by the authentication method. On the other, Wegman-Carter authentication can be used to conduct quantum key distribution successfully even in the presence of a more powerful adversary, that is, someone who could alter the public channel messages as well as listening to them. Quantum cryptography may also prove useful for protecting private information while it is being used to make public decisions. The classic example of such discreet decision making is the "dating problem," in which two singles seek a way of making a date if and only if each likes the other, without disclosing any further information. For example, if Alice likes Bob, but Bob does not hke Alice, the date should be called off without Bob's finding out that Alice likes Wm (on the other hand, it is logicaUy unavoidable for Alice to learn that Bob does not like her, because if he did the date would be on). There are many other situations in which joint decision making between corporate or governmental orga@zations or between an individual and an organization depends on confidential information that the negotiating parties wotfld rather not disclose in full. A discreet solution to the dating problem, or any other joint decision depending on private data, can be obtained by having Alice and Bob confide their private data to a trusted intermediary (Eve, for example) and letting her make the decision. The hazards of this approach are obvious: Alice and Bob must trust Eve both to make the decision correctly in the first place and never to reveal the private data. Various other techniques allow public decisions based on private inputs to be made without a single trusted intermediary. For example, a successful protocol can be set up among niany participants that will fail only if a majority of the participants conspire to spoil the output or reveal the inputs. On the other hand, if two parties believe in the security of public-key cryptosystems, they can make decisions discreetly without any intermediary. in 1982 Andrew C.-C. Yao, then at Stanford University, was one of the first to investigate tws problem. Recently Claude Crepeau of the Ecole Normale Superieure and CNRS and his student Marie-Helenene Skubiszewska, in collaboration with two of us (Bennett and Brassard), have shown that a quantum apparatus similar to the one already built for key distribution can be used to make joint decisions discreetly without intermediaries and without unproved mathematical assumptions. Discreet decision making can be implemented by repeated application of a curious information-processing procedure called oblivious transfer. The procedure is a version of Wiesner's feat of sending two messages in such a way that the receiver can read either one but not both. hi 1981 Michael 0. Rabin of Harvard University formalized the notion of oblivious transfer, unaware of Wiesner's pioneering but unpublished work a decade earlier. Later, Crepeau, Joe Kilian, then at the Massachusetts Institute of Technology, and others demonstrated that oblivious transfer could be apphed to discreet decision making. One particularly attractive feature of discreet quantum decision making is that, unlike key distribution, it is worthwhile even over short distances. Unfortunately, known implementations are mathematically rather inefficient, requiring many thousands of photons to be sent and received to reach even simple decisions. If its mathematical efficiency can be sufficiently improved, discreet decision making may become the most important application of quantum cryptography.
The Cipher of Che Guevara
When in 1967 the Bolivian army captured and executed the revolutionary Ch6 Guevara, they found on his body a worksheet showing how he prepared a message for transmission to Cuban president Fidel Castro. Guevara used the unbreakable cipher invented by Gilbert Vernam in 1918. The letters of Guevara's message (in Spanish) were first translated into oneand two-digit decimal numbers by a fixed rule, namely
![]()
By itself this procedure would have provided virtually no protection. The message digits were then strung together in convenient five-digit blocks.
They became the top line of each three-line group on the worksheet. The middle line of each group is the key, a sequence of random digits known only to Guevara and Castro.

Next the message and key were added (without carries) to produce a cryptogram, forming the bottom line of each three-line group. Because of the addition of the random key digits, this cryptogram is itself a random decimal sequence, carrying no information about the original message, except to someone who knows the key. The cryptogram was then transmitted to Cuba by an insecure channel such as shortwave radio. At the receiving end, Castro's cipher office would have subtracted the same random key digits, reconstructing the number sequence in the top row, and then would have translated the numbers back into the letters of the message. Many spies and diplomats have used the Vernam cipher throughout the 20th century. The key, rather than consisting of decimal digits, can be a long random sequence of the binary digits 0 and 1, and the additions and subtractions would be carried out in base 2 by machine, rather than in base IO by hand. Nevertheless, the key must still be hand-carried from the place where it is generated to the places where it will be used, and it must be assiduously guarded during all phases of delivery and storage to prevent it from falling into the hands of an adversary.
Quantum Cryptography Scientific American May 89
Single-photon communications can outwit eavesdroppers
For as long as mathematicians have been creating ciphers to Fkeep messages secret, other mathematicians have been breaking them. Whenever an eavesdropper intercepts a message, its encoding algorithm and key can eventuaill be deduced and the secret compromised. Matters have improved a bit in the 1980's. With the Data Encilption StandarcL knowing the algorithm purportedly offers the code breaker no help, and with public-key crptosystems, even knowing half of the key is not enough to break a cipher quickly.
A new technique called quantum cryptography takes another approach: an eavesdropper cannot even listen in on a message without alerting the sender and receiver to the attack. There are a few hitches, of course - transmission is slow, the system can operate over distances of a few kilometers at best and only random bits can be communicated. Developed by Charles H, Bennett of the IBM Thomas J. Watson Research Center and Gilles Brassard of the University of Montreal, quantum cryptography relies on the fact that measuring a quantum-mechanical system such as a photon irrevocably changes its state and destroys information about the details of the state before measurement. An eavesdropper must make a measurement to gain information, and so any eavesdropping scrambles the original message. In the physical setup developed by Bennett and Brassard, the "quantum channel" consists of a device that sends single photons whose orientation is either rectilinear (vertical or horizontal) or diagonal (45 or 135 degrees from the horizontal) and a detector at the other end that reads the polarization of incoming photons. If the photon and the detector are both oriented in the same fashion (whether rectilinear or diagonal), the detector will be able to determine the polarization (vertical or horizontal, 45 or 135 degrees) correctly but if the two are oriented differently the results will be random: a diagonal photon always has a 50-50 chance of passing through a rectilinear detector, and vice versa. To communicate the sender transmits a string of bits in a random series of orientations. The receiver chooses another random series of orientations for detection. After the transmission the receiver reports to the sender, through a conventional channel, the series of orientations selected for detection; the sender says which ones were correct. The resulting set of bits, known to both sender and receiver but to no one else, can then serve as a key for a conventional encryption scheme capable of sending actual messages. An eavesdropper trying to measure photons and then retransmit them has an even chance of choosing the wrong orientation and thus passing on a photon that will be read by the intended receiver-using the correct orientation-but will produce a result that does not match the sender's. Any tampering would thus be readily detectable. Noise could mask some eavesdropping, but Bennett, Brassard and jean-Marc Robert of McGill University in Montreal have worked out error-correcting techniques that make such eavesdropping ineffective. How might all of this work in the real world? Photomultipliers can detect a photon every 20 to 50 nanoseconds, and so the basic transmission rate is about 20 millon pulses per second. but as Bennett points out, each pulse should be attenuated to an average of about .1 photon to reduce the probability of generating a two-photon pulse that could be split and eavesdropped undetectably. Half of the pulses will be thrown away because they have been read in the wrong orientation, and photo-multiplier tubes are only about 30 percent efficient in any case. The net rate is perhaps 300,000 bits per second-before factoring in random noise-and the range for sending a single photon is a few kilometers at best. Bennett has set up a demonstration system, and Brassard is writing the software. They expect to transmit a few thousand bits per second early this summer, enough to show that the idea works. Although quantum cryptography may be impractical, Bennett says, the concept of security guaranteed by physical laws is both appealing and intriguing. -Paul Wallach