 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes live video seminars, enchanting renewal songs and a thousand page illustrated codex.
 Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Get the Genesis
of Eden AV-CD by secure
internet order >> CLICK_HERE
Windows / Mac Compatible. Includes
live video seminars, enchanting renewal songs and a thousand page
illustrated codex.
 Return to Genesis of Eden?
Return to Genesis of Eden?
A Quantum Revolution for Computing New Scientist 24 Sept 94
By harnessing the bizarre properties of the quantum world, physicists believe they could construct a computer with undreamt-of power. Julian Brown explains how it might be done. Julian Brown is a science writer and co-author of The Ghost in the Atom, published by Canto in 1993.
AT KEY points in human history, civilisation has advanced as people discovered a new way of exploiting nature. Urban society began when hunter gatherers leamt how to farm land and domesticate animals. The control of steam power led to the Industrial Revolution. And the electronic computer began the information revolution. Could yet another step of comparable magnitude be awaiting us? According to the physicist David Deutsch of Oxford University it is, and he thinks it will come through the creation of a revolutionary new computing machine. The machine is the quantum computer. It would represent a leap forward, Deutsch claims because it relies on aspects of nature that are at the moment totally unexploited. These aspects concern the strange, some would say bizarre properties of matter found at the quantum or atomic level. Deutsch has believed for years that a quantum computer could do things undreamt of by today's computer pmgrammers. Now we have an idea of what these tasks might be: Peter Shor, a computer programmer at AT&T's Bell Laboratories in New Jersey, has devised the first quantum computer algorithm that has powerful applications. If a quantum computer can be built, the algorithm would allow it to break "uncrackable" secret codes in seconds. The idea of the quantum computer emerged in the early 1980s, when scientists were pondering the fundamental limits of computing. They realised that as engineers try to pack ever more logic gates and other circuit elements onto silicon chips, they will eventually reach a point where the logic gates are so small that they are made out of only a handful of atoms. And there the scientists saw a problem. On the atomic scale, matter obeys the rules of quantum mechanics, which are quite different from the classical rules that regulate the properties of conventional logic gates. That raised the question of whether some new kind of computer could be based on quantum principles. Richard Feynman, the late, renowned physicist from the California Institute of Technology was one of the first to try to find out. He produced an abstract model which showed, in principle, how a quantum system could be used to do computations. He also showed that this machine would be able to act as a kind of simulator for quantum physics. in other words, you would be able to carry out experiments in quantum physics inside his quantum mechanical computer. That was interesting in its own right, but it was Deutsch who realised how this could lead to a general purpose quantum computer. In 1985, he published a crucial theoretical paper in which he showed that any physical process could, in principle, be modelled perfectly in a quantum computer. Furthermore, because of this property a quantum computer would be able to do things that no traditional machines could do. This, he argued, was beacause they would be able to exploit the phenomenon of quantum parallelism.
To understand quantum parallelism it helps to look at the famous double-slit experiment carried out by Thomas Young in 1801. Young projected a point source of light onto a plate that was pierced by two narrow slits, close together. As light passed though the slits and towards a screen it produced a pattem of fringes. Such fringes, Young reasoned, are caused by the destructive and constructive interference of light waves traveffing from each of the two slits.
Light spots
However, we now know that light also exists in the form of particles, called photons. In modem versions of Young's experiment it is possible to study what happens when individual photons pass through the two-slit apparatus. An extraordinary state of affairs emerges. During its journey from the source to the screen, each photon somehow travels through both slits simultaneously-yet whenever a photon is actually observed on the screen it only ever appears as a single tiny dot. Although the two-slit experiment remains a puzzle, there are several ways in which physicists have tried to make sense of it. The traditional explanation has been to say that quantum objects like photons can behave like waves or like particles, depending on the circumstances. A radical alternative favoured by people like Deutsch is known as the "many universes" interpretation. In this you have to imagine that all quantum systems exist in multiple or parallel universes. When a single photon passes through the two slits, what happens is that in one universe the photon passes through one slit, and in another universe it passes through the other slit. The photon thus exhibits quantum parallelism by doing different things in different universes In his 1985 paper, Deutsch explored the idea that just as a photon can travel along multiple paths in the two-slit apparatus, so it should be possible to get a computer to compute along different paths in parallel universes. The result would be that a small quantum computer could behave like an immense parallel processing machine. However, there is one major limitation: you can't look at the results of each computational path separately because they are all in different universes. The only way you can take advantage of the simultaneous calculations is to let the universes interfere with each other. This is done by making a measurement. In the two-slit experiment, interference occurs when we observe the position of photons as they arrive on the screen. Likewise, in a quantum computer interference would be achieved by observing the result of a calculation. What you get is not the result from just one universe but a sum over all universes.
After Deutsch published his 1985 paper, the hunt was on for something interesting for quantum computers to do. Unfortunately, all that could be found were a few rather contrived mathematical problems. Quantum computers seemed little more than an academic curiosity. If they were to have any future they needed a 'killer application - something useful that only a quantum computer could do.
This is exactly what Shor has now provided. Earher this year he circulated a preprint of a paper in which he set out a method for using quantum computers to crack an important problem in number theory which has powerful real-world applications. Shor had assembled a toolbox of mathematical operations that can only be performed on a quantum computer. He then showed how these operations could be organised to enable a quantum computer to factorise huge numbers extremely rapidly, much faster than is possible on conventional computers. The reason this is so important is that one common method of encryption relies on the extreme difficulty of factorising very large numbers. Shoes algorithm suddenly raised the possibility that any one who gets their hands on a quantum computer wiff be able to crack the secret transactions of governments, the armed forces and banks. The encryption method is known as RSA, after its three inventors from the Massachusetts Institute of Technology, Ronald Rivest, Adi Shamir and Leonard Adleman. It relies on the fact that it is very much easier to multiply two large prime numbers together than it is to factorise the resulting composite number. When Rivest and his colleagues created the system back in 1977 they challenged anyone to factorise a particular 129-digit number, now known in the trade as RSA-129. The challenge stood until this year, when the number succumbed to the efforts of over 1600 computers hooked up via the Intemet. Even with all that power, it proved a Herculean task lasting more than eight months. Despite this breakthrough, cryptographers reassured them- selves with the thought that they could always add more digits to their codes. The problem of factorising numbers gets exponentially harder the bigger they are. But then Shor dropped a second bombshell. "If we could build a quantum computer that ran as fast as a modern PC, it would be able to factorise RSA-129 in a few seconds," he said. "It does this by trying out many different numbers at the same time. The surprising thing is only the numbers that lead to the right answer constructively interfere. All the other numbers cancel each other out.' Shor's procedure calls an immense number of parallel universes into play to assist the calculation. It does this by putting into a memory register not one number at a time, as in a conventional computer, but-simultaneously- all the numbers that the register could hold. Thereafter calculations on every number proceed in parallel (see Box "Shor's algorithm").
Quantum leap
Such ideas sound incredible, so how could such a machine actually be built? One possibility is to use 'quantum dots': single electrons trapped inside a cage of atoms. When a single dot is exposed to a pulse of laser light of precisely the right frequency and duration, its electron is kicked into an excited energy state. An additional pulse of light knocks the electron back into its ground state again. In a quantum computer the ground state and excited state of the electron would be used to represent 0 and 1 just as in standard binary computing. Thus a single quantum dot can act as a 1-bit memory device or register. It also behaves like a NOT gate, because a pulse of laser light turns a 0 signal into a 1, or a 1 signal into a 0. Using a more elaborate arrangement involving pairs of quantum dots it is possible to create more powerful logic functions, such as one called the Controlled NOT. This is a NOT gate in which one bit is flipped by the action of the laser light only if another bit has previously been set to 1. Despite the unfamiliarity of the technology, such logic functions are similar to those of conventional computers. But there are things you can do with these quantum dot structures that cannot be replicated by classical systems. It is here that we enter the strange world of quantum computing. Consider the NOT gate again. The requirement is that you shine laser light of the right frequency for precisely the right length of time to cause the bit to flip. What happens if you shine the light for only half the prescribed time? According to quantum mechanics the quantum dot goes into what is called a "superposition of states"-a mixture of both the excited and ground states. In the many universes interpretation, this simply means that in one universe the quantum dot is in the ground state and in the other it is in the excited state. Deutsch calls this function the square root of NOT because if you repeat the operation you get a NOT: root(NOT) * root(NOT) = NOT
Building blocks
Something similar can be done with the Controlled NOT function. By halving the time for which laser light is shone it is possible to create -root(Controlled NOT) - The importance of these root functions is that they have no analogue at all in conventional computers. Armed with these and a few other logic functions made from pairs of quantum dots you have all that you need to construct a complete quantum computer. However, quantum dot technology presents two major problems. To build a complete quantum computer you would need to use more than 100,000 dots on a single chip. That is way beyond anything that is possible at the moment. There is also a big difficulty with the machine's computation time. Unfortunately, the electrons in quantum dots tend to stay in their excited states for only around a micro-second. As each burst of laser light lasts around 1 nanosecond, there is only time for around a thousand logical operations before any numbers are erased from the machine. This puts a severe limit on the length of any quantum calculation. After learning of Shor's algorithm, Deutsch along with Arthur Eckert and Adriano Barenco, two fellow physicists at Oxford, tried find a way of overcoming these problems. They noticed that they could streamline the computation of Shor's algorithm by stripping out a lot of the computer's circuitry. The result is a machine that they have dubbed the "factorisation engine" in homage to Charles Babbage and his "analytical engine", the mechanical forerunner of the modem computer. Deutsch estimates that a factorisation engine could be built using as few as 20 dots if you wanted to factorise numbers between 1 and 8 as a test case, and around 2000 dots to factorise RSA-129. How realistic is their idea? At the moment quantum dots are tricky to make because they are so small-typically 1 nanometre across, roughly the size of 10 atoms. Nevertheless, the Japanese electronics company Hitachi is known to be secretly studying quantum dots in the hope of producing a new wave of ultra-high-density memory chips. The technology may arrive sooner than we think. The factorisation engine also calls for state-of-the-art laser technology. To avoid having to squeeze thousands of lasers into a tiny space, each dot would probably be fabricated to respond to its own unique frequency. That way a single laser could be used to control a large number of dots, as long as it could be rapidly tuned and retuned to precise frequencies, according to instructions contained in the factorisation engine's program. According to Eckert there is nothing in principle that should prevent such lasers being produced. "I am quite optimistic about the feasibility of these ideas. The biggest problems are going to be in the nano-structure fabrication, because the elements like quantum dots need to be so pure, so isolated and so well designed. But progress in nanotechnology is very fast." Some scientists are more sceptical. Chief among them is Rolf Landauer of IBM's research centre in New York, one of the leading thinkers on the quantum limits of computing. He has written several papers arguing that quantum computers are likely to be swamped by noise caused by thermal vibrations and defects in construction. However, Deutsch says that it does not really matter if the factorisation engine makes mistakes. "Even if it only works 0-1 per cent of the time correctly, Shor's algorithm is so fast you can afford to run the engine a thousand times or more to make sure you get at least one satisfactory run. It's very easy to check each answer and see whether it is indeed a prime factor of your initial number. If it isn't, you just keep the engine running until you get the right answer."
Uncertain future
The debate over noise remains unresolved. If the problem can be overcome then the question is what other applications can be found for quantum computers. The notion of quantum parallelism might suggest that they would come into their own for tasks such as weather forecasting and running climate models, where vast amounts of number crunching are involved. However, it is far from dear whether the restricted form of parallelism in quantum computers would be suitable for these sorts of problems. Nevertheless, Deutsch is convinced that they will be able to do remarkable things. "Imagine if we had asked some- one in Charles Babbage's day what use computers would be. The answer would probably have been 'Well, we'll be able to calculate logarithm tables more easily'." Nobody could have guessed at modern computer applications such as wordprocessors, payroll programs, databases, factory robots and computer networks. Deutsch believes that the fac- torisation engine could be the first glimpse of a wave of similarly spectacular applications in the 21st century.
Shor's algorithm
THE PROBLEM Shor sets out to solve is how to factorise a large number n that is the product of two prime factors. His procedure depends on some technical results from the mathematics of number theory but it can be summarised in three stages. The first involves taking a memory register and placing in it a quantum superposition of all the possible integer numbers it can contain. this can be done by loading the register with a full set of 0s and then applying a square-root-of-NOT function to every bit. Imagine a two-bit register, for example. After such procedure each bit will be in a superposition of 0 and 1 states. The result is four different parallel universes, one containing a register with 00 (binary for 0), another with 01 (binary for 1), one with 10 (binary for 2) and finally one with 11 (binary fbr 3).
The second stage is an arithmetical operation that takes advantage of quantum parallelism by perfoming a different calculation in each universe. Choose a random number x between 0 and n, then raise it to the power of the number in the register. Divide by n, and place the remainder in a second register. It turns out that for increasing powers of x, the remainders form a repeating sequence. Because the number in the first register is different in each universe the result varies from universe to universe. As an example, take the very simple case where the number you are trying to factorise is 15, and x = 2. The powers of 2 give you 2, 4. 8, 16, 32, 64, 128, 256 ... Now divide by 15, and if the number won't go, keep the remainder. That produces a repeating sequence 2, 4, 8, 1, 2, 4, 8, 1 ...
Stage three is the most complex and depends on the fact that the frequency of of these repeats can be made to pop out of a calculation by getting the different universes to interfere with one another. A complex series of quantum logic operations has to be performed and interference then brought about by looking at the final answer. The final observed value, the frequency f, has a good chance of revealing the factors of n from the expression x^(f/2)-1. in the simple example above, the repeat sequence is the four values 2, 4, 8, 1, so the repeat fiequency is 4. Thus Shor's algorithm produces the number: 2^(4/2) -1 = 3 which is a factor of 15. The method will not always work and in some cases will give a multiple of a factor. But if the result turns out not to be a factor of the original number, the whole three step process can be repeated using a different x. It will on average only take a few trials to factorise n, even when n is hundreds of digits long.
It Takes Two to Tangle Ben Stein New Scientist 29 Sept 96
IN HUMAN relationships, you niay never know what your partner is thinking. But for a pair of quantum particles, even a brief encounter can create a mutual telepathic bond. Before being measured, both particles are in a fuzzy, undefined state, yet they still have a special relationship. When the state of one is measured, the state of the other is instantly defined-even if it is halfway across the Universe. In the strange lexicon of quantum physics, the two particles are said to be 'entangled", a term coined in the 1930s by the German physicist Erwin Schrodinger- But it's not just particles-be they electrons or photons of light-that can be entangled. Different properties of the same particle can be hitched in this way. Indeed in theory, entanglement can create an inimate bond between any quantum systems that have interacted. Physically it means that if you perform any kind of measurement it has an effect on the other even if they are separated by a large distance," says Serge Haroche of the Ecole Normale Superieure in Paris.
For sixty years, entanglement has been at the heart of a philosophical debate over the nature of the quantum world. But in the past few years there has been a profound change in the way that physicists view entanglement. it is now an effect that can be put to work in machines. In the late 1980s, theoreticians found practical ways to exploit entanglement in entirely new concepts, such as quantum connumication and quantum computing. And just in the past few months, experimentalists have taken these ideas even further by building devices such as quantum logic gates, the basic components of quantum computers, and transmitters that can cram ever larger amounts of information on a single photon.
Entanglement is probably best known for its role in the famous debate between Einstein and the Danish physicist Niels Bohr over quantum physics. Einstein could not cope with the fuzziness of the world predicted by the new theory. in that world, for example, an electron in an atom has no definite position, only a range of possible locations, each described by a different quantum state. At best the theory can give the probability that the electron is in one of those states. The conventional quantum mechanical view of this situation is that the electron is not in one place but in all locations at once-it is in a "superposition" of states.
What's more, it is meaningless to try to describe the electron's position until a measureement is made. At that point, the measurement destroys the superposition and forces the particle to occupy a definite position. Einstein disagreed with this interpretation. In his mind, underlying quantum,theory there had to be a world in which a particle's properties-such momentum and position had real pre-existing values. And in 1935, Einstein and two colleagues Boris Podolsky and Nathan Rosen, placed entanglement centre-stage in a thought experiment designed to show that quantum theory gave an incomplete view of reality ("The thought that counts", New Scientist, 6 May 1995, p 26). They argued that the tie which binds entangled particles was a physical impossibility because it appeared to act instantaneously and no knowln influence could travel faster than the speed of light. Einstein dubbed it "Spooky action at a distance" Bohr saw entanglement as a fact of life. Entangled particles are essential parts of the same quantum system no matter how far apart they are, he said. Although no signal passes between them, and no matter how far apart they are they do cooperate upon the act of measurement: knowing the quantum state such as the position, of one particle tells you the state of the other.
However strange this interpretation may seem, most physicists were happy although arguments persisted, and still do today. Yet it was not until 1982 that Alain Aspect of the institute of Optics in Orsay, near Paris, built a real version of the thought experiment. It produced convincing figures to support Bohr's view.
Today researchers are building ever-truer versions of the EPR experiment to probe the boundary between the classical and quantum worlds. But something else happened in the 1980s. Theoreticians began to realise that entanglement could be put to good use beyond understanding quantum theory.
Most of the drive to exploit entanglement sprang from a single idea quantum computing. Paul Benioff of Argonne National Laboratory, Illinois, started investigating the idea of computers that would operate solely at the quantum level by harnessing entanglement. Charles Bennett of IBM's Watson Research Laboratory at Yorktown heights, New York, and particulariy David Deutsch from the University of Oxford took these ideas further. Then in 1994, Peter Shor of AT&T Bell Laboratories in New Jersey caused a stir by presenting the first algorithm for a quantum computer. It described how a device would find the factors of extremely large numbers within seconds. lt would be a formidable tool, capable of cracking even the most secret codes in seconds. Shor's paper had a massive impact, says Williani Wootters, a physicist at Williams College in Williamstown Mass. "That was the trning point there is no question about it" he says "Many people started working in the filed after Shor's discovery.
Pumping digits
The building blocks of a conventional computer are logic gates, which carry out simple operations on the 1s and Os used in binary machines. A NOT gate, for example, switches a 1 to a 0 and vice versa. An AND gate, which has two inputs, sends out a 1 only when both inputs receive a 1: otherwise it sends out a ). Conventional computers register 1s and Os as the presence or absence of electric current, and their logic gates are made from arrays of transistors. They deal with complex calculations by pumping digits through a series of different gates. The hallmark of a quantum computer, however, is that it would process superpositions of 1s and Os. The input data would be converted to superpositions and processed by quantum logic gates, and the result would emerge as a superposition of every possible outcome of that computation. "A quantum computer would in a sense be doing all calculations at the same time, says Wootters. Deutsch calls this phenomenon quantum parallelism ("A quantum revolution for computing", New Scientist, 24 September 1994, p 21). There is a snag, however. To read the result there needs to be a measurement which would destroy the superposition. Every bit of data would be forced to occupy a definite quantum state - a 0 or a 1. So any potential soltitions that included the opposite digit-a 0 or a 1-would be lost. To get round this obstacle, Shor proposed to retrieve his results by allowing all the components of the final superposition to 'interfere" with each other. Two interfering beams of light, for example, can be used to measure tiny changes in distance. They prproducee a pattern of light and dark bands, wiiicii changes when the path length of one beam changes. SShor reckoned that the results of his quantum computations would emerge in a similar way from his interference pattern. Shor's algorithm is fine in theory, but it cannot be tested because there are no machines on which it can run. This could be about to change however. In the past few months researchers have shown how to build quantum logic gates. Devices have enierged partly because of the huge leaps made in controlling the quantum world. Today, physicists can command lasers to cool atoms, trap individual atoms or ions, and "tickle" single quantum states of these particles. Last December, Kimble and his colleagues described a gate that entangles two photons. They use a single caesium atom within an optical resonator, a tiny cavity made of two mirrors that reflect photons back forth, maximizing the chances that they will interact with the atom's other electron. In Caesium this electron can exist in different energy levels. it jumps between two levels if it receives a photon with energy equal to the energy difference between them. Kimble's group exploits a curious energy transition within caesium that is sensitive to a photon's polarisation. Polarisation relates to the direction in which the photon's electric field oscillates. A photon is said to be circularly polarised if its field rotates so that it carves out a helix as the photon moves forward. The researchers found an electron transition within caesium that responds only to photons with an electric field that rotates clockwise-not anticlockwise. Now think of a photon with an electric field that turns clockwise is a 1 and anti-clockwise is a 0. Kimble's group fired pairs of these photons into the cavity and analysed polarisations on the way out. They found the three photon pairs 0-0, 0-1 and 1-0 interacted in an remarkable way. But the pair underwent a more surprising change. In quantum physics, particles such as photons and electrons are described mathematically by a "wave-function", which has peaks and troughs like any other wave. When the pair emerged from the cavity, the phase the phase of the wave-function, the positions of the peaks and troughs had shifted. "Both photons interact with one another by the medium of the atom" say Kimble.
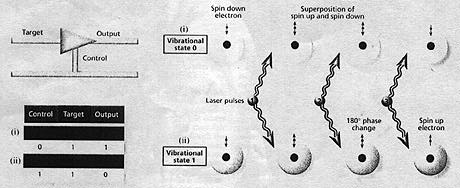
Flipping bits:The behaviour of a controlled NOT
gate (top left) depends on the bit (ed Into the control (bottom
left). In the quantum version of the gate (right), the control
bit Is defined by the vibrational state of a beryllium ion and
the target by the electron's spin.
Photons can also have electric fields that vibrate only in one plane, known as horizontal or vertical polarisations. These can be viewed as superpositions of different states of circularly polarised light-in other words, superpositioiis of Os and 1s. If two of these were sent through the cavity, the "1-1 components" of these superpositions would interact to change the wavefunction's phase, while all the other interacting components would produce unremarkable results. The photons leaving the cavity would then be in a complex superposition of the two original superpositions. They would be entangled. Gates that take 1s and Os and use them to change the phase of a wavefunction in this way may have applications in analogue computing, says Kimble. Most machines designed to deal with Shor's algorithm, however, use gates that flip 1s to 0s or vice versa, as a conventional computer does. Thisis what Dave Wineland and his group at the Nationa Institute of Standards and Technology at Colorado, have set out to do. They have built a controlled NOT gate, which flips a "target" bit from 0 to 1 or vice versa only when a second input, called the control, receives a 1 (see Diagram). if the control bit is a 0, then the target's output stays the same as its input. Like Kimble's gate, Wineland's can also process superpositioiis of 1s and Os. "The controlled NOT gate is the fundamental entangling gate," says Chris Monroe, a member of the NIST team. The NIST team has entangled two quantum systems within the same object-a positively charged beryllium ion. First, the researchers trap the ion in a web of electric fields known as a Paul trap. The electric forces push the ion towards the centre, where it vibrates. They then cool the ion to 1 millikelvin, which robs it of nearly all its motion, and screen out any interference. The ion's vibrational energy level provides the control bit. An ion in the lowest vibrational state is a binary 0. An ion in the next highest vibrational state is equivalent to a 1. The target is provided by the other electron, which can exist in one of two energy levels, depending on the electron's "spin". Spin is a quantum mechanical term analogous to the angular momentum of a spinning top, and in this case comes in two values-spin down and spin up. Wineland and his team can switch the electron between these two states with laser pulses. Hit it once and the electron jumps to spin up, for example, hit it again and it jumps back down. The length of the laser pulse is also important. If a time t is needed to make the electron switch states, then 2t will take it to the other energy level and back to its original state. Weirder still, t/2 will leave the electron in a superposition of spin-up and spin-down states. So how does the gate work? Let's assume the electron is spin down and the vibrational state is 1. The researchers apply three laser pulses (see Diagram top left). The first lasts for t/2 and puts the electron in a superposition of spin-up and spin-down states. The middle pulse exploits a peculiarity of the experimental setup. On top of the two spin states, the electron has a third energy level and the energy required to reach it depends on the ion's vibrational state. The energy of the middle laser pulse is tuned to make the electron jump to this third level only if it is in its spin-up state and the ion is in vibrational state 1, so only this component of the superposition is affected. But there is an added twist. The middle pulse is on for 2t. "it takes the electron up and all the way back," says Dawn Meekhof, another member of the team. When the electron returns, the phase of its wavefunction is shifted through 180 degrees, she says. A 180 degree phase shift means that the wave's peaks are where the troughs were and vice versa.
Awesome series
The third laser pulse, like the first, lasts for t/2. lt completes the electron's transition to the spin-up state. So, the gate has flipped the electron from spin down to spin up-analogous to flipping a 0 to a 1. If the ion's vibrational state is 0, the middle pulse has no effect on the electron. And without the 180 degree phase change, the electron does not jump to spin up when hit by the third pulse, but falls back to spin down. This is equivalent to "0 in, 0 out". In fact, the NIST team has shown that its gate works in the same way as a classical controlled NOT gate. Now imagine an experiment in which the vibrational state starts off in a superposition of states 0 and 1, and the electron begins in the spin-down state. As the laser pulses are fired, the ion travels through an awesome series of superpositions, ending up in the not-too-frightening super-position of vibrational state 0 spin-down and virbrational state 1 spin-up. The vibrational and spin states are now entangled: if you measure the electron's spin to be down, for example, you know the vibrational state is 0. ctors This result also shows Deutsch's concept of quantum parallelism in action. The gate has not just performed one controlled NOT operation, but two. The target bit has been processed as though the vibrational state (the control bit) were set at both 0 and 1. Of course, a functioning computer would need more than a single gate and mathematicians would need many inputs to carry out parallel processing. At present, however, researchers have managed to entangle only two quantum systems. Both Wineland's and Kimble's groups have plans to entangle several quantum systems at once. But even if these experiments succeed, practical quantum computation could still be some way off. Haroche says that to factor a number like 15 would take. 20,000 logic gate operations on 20 entangled particles. To handle the extremely large numbers envisioned by Shor would take many times more operations and gates. Entangling just three particles would be an 'experimental tour de force", he says. Monrue also stresses that it's early days. "We're just trying to understand this thing called entanglement," he says. Another area in which entanglement can be exploited is quantum communication, a way to send data more efficiently than by conventional means. Today's digital telecomniuiiications are limited to sending one of two bits at a time a 0 or a 1. The same holds for an atom that, say, can exist high energy state. But in 1993, Bennett and Stephen Wiesner formerly at Columbia University, New York, realised that if such a two-state particle is a member of an entangled pair, it can send up to four different digits-0, 1, 2 and 3. Using binary it takes eight bits to transmit one of the 256 characters in the ASCII computer code. But for an entangled particle capable of conveying one of four digits the same job could be done with 4 particles. In June, Jaraid Weinfurter at the University of Innsbruck in Austria and his team published results showing that they had moved part way towards this goal by encoding one of three digits-or trits, as they call them-onto a single entangled photon (Science, Netv Scientist, 6 July, p 16). They sent an ASCII character using 5 trits instead of 8 bits. Weinfurter's team generate the entanglement by passing a single ultraviolet photon through a material called barium borate, which splits single photons into two photons, one polarised horizontally, the other vertically. These photons are entangled because it is impossible to tell which is polarized horizontally and which vertically until a mesaurement is made. One photon passes through an encoder where it undergoes one of four operations, each of which represents a digit. The photon may have its polarization flipped or its phase changed, or a combination of the two; or it may be left alone. The two photons are recombined and sent to the recipient, who has an array of detectors (see Diagram).
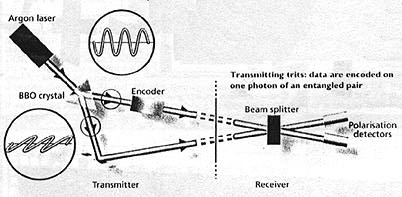
Transmitting trits: Data are encoded on one photon
of an entangled pair.
The group analyses how each entangled photon interferes with its partner to reveal the encoding added at the transmitter and hence the digit it carries. Although Weinfurter used four distinct changes to encode his signal, two of them appeared the same to the detectors. This meant he could only assign one of only three digits to each photon. Quantum communication is still in its infancy, so it's likely to be many years before the phone company starts sending entangled pairs down its fibre optic cables. The potential, however, is enormous, says Wootters, because it is possible to cram even more than four digits on an entangled particle. If the quantum system has three distinct states, you can theoretically encode up to nine different messages. But once again, the spanner in the works is how to entangle more than two quantum systems. Many physicists remain sceptical about the prospects of such schemes. Haroche feels that entangle ment will always be on a small scale-perhaps no more than a few dozen entangled systems. Entanglenient is extreniely fragile, says Haroche. Disturbing one member of an entangled pair will destroy any superposition . Making a measurement is one way to do this, but "noise" is more insidious. Tiny movements of an ion in an electric field trap, for example induce currents in the trap's electrodes which draw energy from the ion and destroy any entanglement. This decoherence is the arch enemy of entanglement and is eventually inevitable. And if you tried to entangle 10 photons, "you will have to look for the entanglement 10 times faster" before decoherence sets in, says Haroche. But other physicists believe decoherence can be defeated by quantum error correction. Just as in conventional error correction, this means storing the same bit of information in several places. Entangling these redundant bits would allow researchers to detect if any had become corrupted. IBM physicist David DiVincenzo is optimistic that quantum error correction can defeat decoherence. "We have been accusiomed to say that entangled states are very delicate and fall apart very easily," he says. "But in the setting of quantum computation, I believe that we will say that the opposite is true. Entangled states can be made very robust." If he is right, we may see quantum computers and quantum communications in the next few years. Whatever the outcome, it seems ironic that entanlement, which Einstein chose as a way to undermine quantum mechanics, today underpins a vast new field of research.
Quantum Leap New Scientist 18 April 1998
THE era of quantum computing has begun in earnest, scientists say. For the first time, they have made a quantum computer that can carry out a task in a way that is impossible with supercomputers. The bits of a conventional computer can only exist in two states, 0 or 1. In quantum computers, the bits (or "quoits") can be the spin states of a proton, for instance, which exist as a "superposition" of both 0 and 1 until a measurement is made ("Wake up to quantum coffee", New Scientist, 15 March 1997, p 28). This allows quantum computers to explore different routes through a mathematical problem simultaneously. In theory, they can quickly perform some tasks, such as factoring huge numbers and cracking ingenious cryptographic codes, that would take a conventional supercomputer years. Lov Grover, a physicist at AT&T Bell Labs in New Jersey, showed last year how a quantum computer could "guess" a chosen number in a certain range. The task is similar to a game of "higher/lower"-homing in on a number by repeatedly asking if the one you guess is too high or too low. Repeated questioning would be all a classical computer could do. But Grover showed that a quantum computer could divine the number in one attempt, just like packing all the questions into the states of a qubit. "It's interesting and kind of surprising that you can somehow do it when you get only one bit out of the computer," says Norm Margolus, a physicist at the Massachusetts Institute of Technology in Cambridge. Now Isaac Chuang of IBM's Almaden Research Center in San Jose and Neil Gershenfeld of MIT have made a quantum computer that works through another of Grover's algorithms, answering two questions about one of four numbers. The problem is similar to asking which of the numbers 1, 2, 3 and 4 is odd and greater than 2. In the current issue of Physical Review Letters (vol 80, p 3408), the researchers describe how they used the nuclei of a carbon atom and a hydrogen atom in a chloroform molecule as two quoits. Both nuclei had spin 0 and spin 1 states, giving four combinations which existed simultaneously: 00, 01, 11 and 10. Using magnetic fields and radio waves, the researchers manipulated the atoms'spins, making them dance a nuclear jig corresponding to the algorithm's logic. The correct answer to the calculation came when a measurement of the spin states "snuffed out" those that did not match the target state. Chuang and his colleagues have since been working on other quantum algorithms, such as the "Deutsch-Jozsa" algorithm, which spots some properties of a mathematical function far faster than a classical computer. Although cracking codes is still years away, Grover says the new work proves quantum computers are no longer just an idea. "It's a remarkable achievement," he says. "They've demonstrated that quantum computing works, not just with pencil and paper, but in the lab." Charles Seite